Теоремы подобия
Первая теорема подобия была сформулирована И. Ньютоном. Согласно теореме, при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы, т. е. подобные между собой явления имеют численно равные критерии подобия. Первая теорема подобия может быть сформулирована также следующим образом: у подобных явлений, индикаторы подобия равны единице. Вторая теорема подобия была доказана Бэкингемом, Федерманом и Афанасьевой-Эренфест. Согласно теореме любая зависимость между переменными, характеризующими какое-либо явление, может быть представлена в виде зависимости между соответствующими критериями в форме уравнения подобия (критериального уравнения). Критерии подобия, которые составлены только из величин, входящих в условия однозначности, называют определяющими. Критерии, включающие также величины, которые не являются необходимыми для однозначной характеристики данного процесса и сами зависят от этих условий, называют определяемыми. Какой из критериев является определяемым, зависит от формулировки задачи. Таким образом, если определяемым является некоторый критерий K 1, то уравнение удобнее представлять в виде степенной функции, выражающей зависимость определяемого критерия К1, содержащего искомую величину, от определяющих критериев K 2, K 3, …, Kn, отражающих различные стороны процесса:
Такие уравнения называют уравнениями в обобщенных переменных (обобщенными) или критериальными уравнениями. Число и вид критериев, необходимых для описания процесса, могут быть во многих случаях найдены чисто аналитическим путем общего вида системы дифференциальных уравнений данного процесса либо на основе теории размерностей. Коэффициенты С, m, n, r, входящие в уравнения подобия, определяются опытным путем. Из критериального уравнения, представляющего собой функциональную зависимость между критериями подобия, рассчитав предварительно значения определяющих критериев, находят значение определяемого критерия, а из него - значение интересующей величины. Вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов, проведенных на моделях: их надо представлять в виде функциональной зависимости между критериями подобия. Другим преимуществом критериальных уравнений является их универсальность, т. к. использование в них обобщенных переменных (критериев) позволяет применять их для целой группы подобных между собой явлений, а не только для данного единичного явления. Третья теорема подобия (теорема М.В. Кирпичева и А.А. Гухмана) формулирует необходимые и достаточные условия подобия явлений: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности. Подобию же условий однозначности при идентичности дифференциальных уравнений, описывающих процессы, отвечает равенство определяющих критериев подобия. Значит, третья теорема подобия может быть сформулирована и так: явления подобны, если их определяющие критерии численно равны. Условиями однозначности называют граничные и начальные условия, позволяющие из бесконечно большого числа решений системы дифференциальных уравнений (неопределенное интегрирование) выделить единственное, отвечающее условиям данной задачи. Критерии, содержащие хотя бы одну величину, не входящую в условия однозначности, называют неопределяющими. Из третьей теоремы следует, например, что для подобия явлений движения жидкости в трубах необходимо, чтобы профили скоростей на входе были подобны друг другу. Критериальные уравнения выражают собой зависимость неопределяющего критерия от определяющих. С учетом постановки задачи в соответствии с конкретными условиями однозначности один и тот же критерий может быть в одном случае определяющим, в другом - неопределяющим.
|

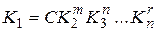 . (13)
. (13)


