Анализ размерностей
Многие процессы пищевой технологии зависят от такого большого числа различных факторов, что для них не удается получить полного математического описания; можно лишь в самом общем виде представить зависимость между различными переменными, влияющими на протекание процесса. Если, некоторая величина K 1 зависит от параметров K 2, K 3, K 4 и K 5, то общий вид зависимости между данными величинами
Для отыскания конкретного вида этой функциональной зависимости, т. е. для нахождения расчетного уравнения, может быть применен метод анализа размерностей. В основу метода положена p -теорема Бэкингема, согласно которой общую функциональную зависимость, связывающую между собой п переменных величин при т основных единиц их измерения, можно представить в виде зависимости между (п - т) безразмерными комплексами этих величин, а при наличии подобия - в виде связи между (п - т) критериями подобия. Так, например, если рассматриваемое явление описывается соотношением (2.14), связывающим пять каких-то физических величин, и если эти величины выражаются посредством трех основных единиц измерения, то п = 5 и т = 3. Следовательно, (п - т) = 2, и указанная функциональная зависимость может быть представлена в виде функции между некоторыми двумя безразмерными комплексами p 1 и p 2:
Структура функции должна обеспечивать свободу выбора единиц всех первичных величин и независимость отношения двух любых значений вторичной величины от выбора этих единиц (принцип абсолютности отношений). Таким свойством обладают только гомогенные функции. Эти функции могут быть представлены только степенными произведениями:
где K – множитель преобразования вторичной величины, ki – множители преобразования первичных величин. Показатель степени ai называется размерностью вторичной величины в отношении данной первичной. Совокупность размерностей принято записывать в виде формулы размерности, т. е. в виде символического уравнения, которое получается из последнего уравнения при замещении множителей преобразования величин их символами. При этом символ вторичной величины обычно берется в прямые скобки. Например, формула размерности для скорости (символ V) записывается в виде
где L – символ длины, Т – символ времени. Понятие размерности условно можно распространить и на первичные величины, считая размерность первичной величины в отношении самой себя равной единице, а в отношении любой другой первичной величины – нулю. При таком соглашении формула размерности первичной величины совпадает с ее символом. Окончательные формулы размерности должны быть приведены к первичным величинам. Например, для силы (символ F) имеем
где М – символ массы; А – символ ускорения. Метод анализа размерностей основывается на следующих положениях. Формулу размерностей производных единиц можно представить в виде степенного комплекса основных единиц. Если обозначить физическую величину через W, ее размерность в СИ можно записать Пусть величина W является функцией n размерных величин W = f (a1, a2,...., an). Можно доказать, что эта зависимость заменится уравнением П = f (1, 1,...., 1, где роль размерных величин играет n-k безразмерных величин. В гидродинамических исследованиях основная система состоит из трех единиц (кг, м, с) значит k= 3, и вместо n величин изучаемое явление представляется в виде зависимости между n- 3 безразмерными комплексами этих величин. Зависимость (19) - то критериальное уравнение, которое исследователь должен установить, анализируя опытные данные в виде комбинаций безразмерных комплексов. Покажем применение метода анализа размерностей на примере определения перепада давлений при движении жидкости в трубопроводе. При этом допустим, что дифференциальное уравнение, описывающее этот процесс, отсутствует. Известно, что при установившемся движении жидкости в прямой трубе перепад давлений Таким образом, известна лишь функциональная зависимость общего вида В данном случае число переменных n = 7, число единиц измерения (длины, времени и массы) k = 3. Тогда, согласно p -теореме, число безразмерных комплексов, описывающих процесс, должно быть равно (n - k) = 4. Представим функциональную зависимость (20) в степенном виде где x, y, z, u, r, s, t - неизвестные числовые коэффициенты. Единицы измерения в СИ и их размерности величин, входящих в (21): Учитывая, что размерности обеих частей уравнения (21) одинаковы, а x - безразмерный коэффициент, заменим в нем все величины их размерностями или при подстановке конкретного выражения размерностей каждой величины получаем Раскрывая скобки в правой части (2.22) и группируя однородные члены, находим Приравнивая показатели степеней при одинаковых членах, т. е. основных единицах в обеих частях уравнения (23), получаем систему В системе (24) из трех уравнений - шесть неизвестных, поэтому любые три из этих переменных можно выразить через три других Подставим значения показателей степеней z, t, y в степенную зависимость (21) Сгруппировав отдельные величины в (25), находим обобщенную зависимость для определения перепада давлений Таким образом, искомая функция, в соответствии с p -теоремой, представлена в виде соотношения между четырьмя безразмерными комплексами величин - критериями подобия Эйлера, Рейнольдса, Фруда и симплексом геометрического подобия. Числовые значения коэффициента x и показателей степеней u, r, s должны быть найдены опытным путем. Величины, численные значения которых не зависят от выбора основных единиц измерения, называются безразмерными. Методы подобия и размерностей тесно связаны между собой и указывают, как должен быть поставлен эксперимент, как составить программу исследований и каким требованиям должна удовлетворять модель, какие величины надо измерять в опытах и какие приборы при этом надо использовать, как следует обрабатывать полученные результаты и на какие явления их можно распространить, как обобщать и анализировать данные экспериментов. Безразмерные степенные комплексы, составленные из величин, существенных для данного процесса, называются числами подобия. Число подобия, содержащее только заданные по условию задачи параметры, называется критерием подобия и обозначается первыми двумя буквами фамилий известных ученых, работавших в соответствующей области.
|

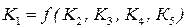 . (14)
. (14) . (15)
. (15) , (16)
, (16) , (17)
, (17)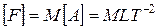 (18)
(18)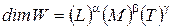 .
.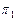 ,
,  ,...,
,..., 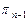 ), (19)
), (19) зависит от скорости жидкости v, ее плотности r, динамической вязкости m, ускорения свободного падения g, длины трубы l и ее диаметра d.
зависит от скорости жидкости v, ее плотности r, динамической вязкости m, ускорения свободного падения g, длины трубы l и ее диаметра d. = f (v, ρ;, μ;, g, l, d). (20)
= f (v, ρ;, μ;, g, l, d). (20)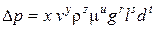 , (21)
, (21)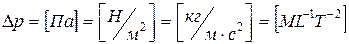 ;
;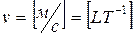 ;
; ;
;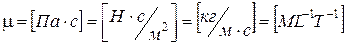 ;
;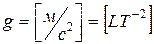 ;
; ;
; .
.
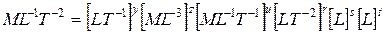 . (22)
. (22)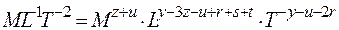 . (23)
. (23)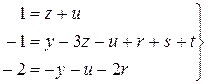 . (24)
. (24)
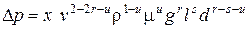 или
или  . (25)
. (25) . (26)
. (26)


