Теория подобия
Теория подобия – это учение о подобных явлениях, т. е. учение о методах исследования явлений в своих, характерных для каждого явления, переменных, представляющих собой безразмерные степенные комплексы, составленные из величин, определяющих сущность явления. Различают подобия: Геометрическое подобие предполагает, что сходственные размеры данного тела и ему подобного параллельны, а их отношение выражается постоянной величиной. В геометрии подобными называются фигуры одинаковой формы, у которых сходственные углы равны, а сходственные стороны пропорциональны. У подобных фигур (рис. 1) отношение сходственных сторон и высот
т. е. представляет собой постоянную величину сl 1, которая носит название константы подобия или коэффициента подобного преобразования.
Рис. 1. Геометрическое подобие С помощью константы подобия можно сравнивать между собой только две подобные фигуры:
Если же в качестве масштаба измерения взять один из линейных размеров треугольника (сходственную сторону или высоту треугольника), то для всех подобных треугольников
где i – инвариант подобия. Временное подобие требует, чтобы сходственные точки или части геометрически подобных систем, двигаясь по геометрически подобным траекториям, проходили геометрически подобные пути в промежутки времени, отношение которых выражается постоянной величиной. Временное подобиесоблюдается, если отношение между сходственными интервалами времени процесса выражается постоянной величиной. Сходственными интервалами времени процесса – это интервалы, в течение которых завершаются аналогичные стадии рассматриваемых процессов. Временное подобие процессов называют гомохронностью (однородностью во времени). Временное подобие характеризуется константой временного подобия:
где Физическое подобие требует, чтобы в рассматриваемых подобных системах отношение физических констант двух любых сходственных точек или частиц, подобно размещенных в пространстве и во времени, были постоянными; Предпосылкой подобия полей физических явлений обязательно должно быть геометрическое подобие, т. е. физические поля подобны, если в сходственных точках геометрически подобных систем отношение физических величин выражено постоянными значениями соответствующих констант подобия:
Подобие начальных и граничных условий предполагает, что начальное состояние и состояние на границах систем подобны при условии наличия геометрического, временного и физического подобий. Безразмерные числа отношений называют инвариантами подобия и обозначают буквой i – первой в слове idem (тоже самое). Если инварианты подобия представляют отношение простых однородных величин, то они называются симплексами. Инварианты подобия, выраженные отношением сложных разнородных величин, называются критериями подобия. Информация, которой должны быть дополнены основные уравнения, описывающие процесс, представляет собой условия единственности решения. Аналитическое исследование уравнений необходимо дополнить граничными условиями. В основных уравнениях не отражено начало процесса, поэтому вводится понятие о начальных условиях. Граничные и начальные условия вместе составляют краевые условия. Кинематическое подобие. Примером может служить подобие движения жидкости (рис. 2). Оно также требует наличия геометрического подобия, т. е. если необходимо изучить распределение скоростей потока жидкости в сечении круглой трубы, то подобный поток должен быть осуществлен так же в трубе круглого сечения. При этом сравниваться между собой должны скорости в точках, отвечающих геометрическому подобию (2). При этом должно быть обеспечено подобие физических полей, т. е. в сходственных точках. В результате можно получить w / w′ = cu. d /4 v
d
Рис. 2. Кинематическое подобие
|

 , (1)
, (1)
 ;
;  . (2)
. (2) ;
;  , (3)
, (3) .
. – интервалы времени в первом процессе;
– интервалы времени в первом процессе;  – интервалы времени во втором процессе.
– интервалы времени во втором процессе. ;
; 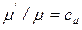 ;
;  ;
;  . (4)
. (4)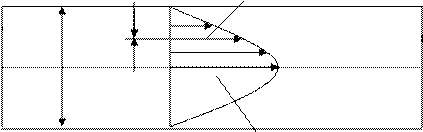
 vmakc
vmakc


