а) Пусть дано уравнение, связывающее две переменные х и у. Если все члены этого уравнения перенести в левую часть, то оно будет иметь вид
 (1)
(1)
Уравнение (1) вообще говоря, определяет одну или несколько функций 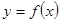 . Например, уравнение
. Например, уравнение  определяет одну функцию
определяет одну функцию  , а уравнение
, а уравнение  определяет две функции
определяет две функции  и
и  .
.
Если в рассмотренные уравнения вместо у подставить найденные функции, то они обратятся в тождества.
Определение: Всякая непрерывная функция 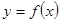 , обращающая уравнение
, обращающая уравнение  в тождество, называется неявной функцией, определяемой уравнением
в тождество, называется неявной функцией, определяемой уравнением  .
.
Не всякое уравнение  определяет неявную функцию. Так уравнение
определяет неявную функцию. Так уравнение  не удовлетворяет ни одной паре действительных чисел
не удовлетворяет ни одной паре действительных чисел  и, следовательно, не определяет неявную функцию. Сформулируем условия, при которых уравнение
и, следовательно, не определяет неявную функцию. Сформулируем условия, при которых уравнение  определяет неявную функцию
определяет неявную функцию 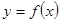 .
.
Пусть дано уравнение (1)
б) Теорема существования неявной функции.
Если функция  и её частные производные
и её частные производные  и
и  определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки  и при этом
и при этом  , а
, а  , то уравнение
, то уравнение  определяет в этой окрестности точки
определяет в этой окрестности точки  единственную неявную функцию
единственную неявную функцию 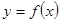 , непрерывную и дифференцируемую в некотором интервале, содержащем точку
, непрерывную и дифференцируемую в некотором интервале, содержащем точку  , причём
, причём  .
.
Геометрически это означает, что в окрестности точки  кривая
кривая  представляет собой график непрерывной и дифференцируемой функции
представляет собой график непрерывной и дифференцируемой функции 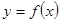 .
.
в) Производная неявной функции.
Пусть левая часть уравнения  удовлетворяет условиям, указанным в теореме, тогда это уравнение определяет неявную функцию
удовлетворяет условиям, указанным в теореме, тогда это уравнение определяет неявную функцию 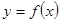 , для которой в окрестности точки
, для которой в окрестности точки  имеет место тождество относительно х:
имеет место тождество относительно х:  . Тогда
. Тогда  , при любом х из окрестности х0.
, при любом х из окрестности х0.
По правилу дифференцирования сложной функции 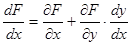
и, значит,  .
.
Отсюда
 или
или  (2)
(2)
По этой формуле находится производная неявной функции (одной переменной 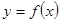 ).
).
Пример: х3+у3-3ху=0
Имеем  х3+у3-3ху,
х3+у3-3ху,  = 3х2-3у
= 3х2-3у  = 3у2-3х
= 3у2-3х
 = -
= -  .
.
Обобщим понятие неявно заданной функции на случай функции нескольких переменных.
Уравнение  (3) определяет неявно заданную функцию
(3) определяет неявно заданную функцию  , если эта функция непрерывна и обращает уравнение
, если эта функция непрерывна и обращает уравнение  в тождество, т.е.
в тождество, т.е.  (4).
(4).
Условия существования и единственности неявно заданной функции формулируются аналогично.
Найдём  и
и  :
:

 = -
= - 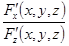

 = -
= - 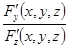
Пример: 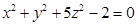

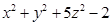
 2х
2х
 2у
2у

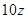
Тогда
 = -
= - 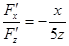 ;
;  = -
= -  .
.

 (1)
(1)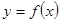 . Например, уравнение
. Например, уравнение  определяет одну функцию
определяет одну функцию  , а уравнение
, а уравнение  определяет две функции
определяет две функции  и
и  .
. не удовлетворяет ни одной паре действительных чисел
не удовлетворяет ни одной паре действительных чисел  и, следовательно, не определяет неявную функцию. Сформулируем условия, при которых уравнение
и, следовательно, не определяет неявную функцию. Сформулируем условия, при которых уравнение  и её частные производные
и её частные производные  и
и  определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки  и при этом
и при этом  , а
, а  , то уравнение
, то уравнение  единственную неявную функцию
единственную неявную функцию  , причём
, причём  .
. . Тогда
. Тогда  , при любом х из окрестности х0.
, при любом х из окрестности х0.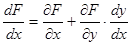
 .
. или
или  (2)
(2) х3+у3-3ху,
х3+у3-3ху,  .
. (3) определяет неявно заданную функцию
(3) определяет неявно заданную функцию  , если эта функция непрерывна и обращает уравнение
, если эта функция непрерывна и обращает уравнение  (4).
(4). и
и  :
:
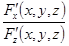

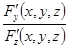
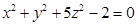

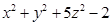
 2х
2х 2у
2у
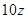
 = -
= - 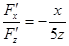 ;
;  = -
= -  .
.


