Преобразование остальных элементов симплекс-таблицы.
Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника». К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки « «х3 Аналогично преобразуются значения других клеток: «х3 х1»: «х4 «х4 х1»: «х6 «х6 х1»: « « В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5). IIитерация: 1 этап: составление симплекс-таблицы. По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу: Таблица 5.5 Симплекс-таблица II итерации
2 этап: определение базисного решения. В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):
Как видно, при данном базисном решении значение целевой функции 3 этап: проверка совместности системы ограничений. Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена. 4 этап: проверка ограниченности целевой функции. Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена. 5 этап: проверка допустимости найденного базисного решения. Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент. 6 этап: проверка оптимальности найденного базисного решения. Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу. 8 этап: определение разрешающего элемента.
|

 », условно обозначим его «х3
», условно обозначим его «х3  .
. ;
; ;
; ;
; ;
; ;
;
 ;
; .
.
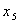













 .
. =15, что больше чем при предыдущем базисном решении.
=15, что больше чем при предыдущем базисном решении.


