Модели транспортной задачи
Для доказательства теоремы необходимо показать, что при заданных условиях существует хотя бы один план задачи и линейная функция на множестве планов ограничена. Доказательство. Пусть Тогда величины xij (2) и (3). Действительно, подставляя значения в (2) и (3), находим Выберем из значений Cij наибольшее C¢ = max Cij и заменим в линейной функции (1) все коэффициенты на C¢ тогда, учитывая (2), получим Выберем из значений Cij наименьшее C C ij и заменим в линейной функции все коэффициенты на C Объединяя два последних неравенства в одно двойное, окончательно получаем C M, т. е. линейная функция ограничена на множестве планов транспортной задачи.
Транспортная задача, в которой суммарные запасы и потребности не совпадают, т. е. не выполняется условие a) суммарные запасы превышают суммарные потребности b) суммарные потребности превышают суммарные запасы Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений. Найти минимальное значение линейной функции xij ³ Открытая модель решается приведением к закрытой модели. В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель Bn+1, потребности которого bn+1 = Стоимость перевозки единицы груза как фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится. После преобразований задача принимает вид закрытой модели и решается обычном способом. При равных стоимостях перевозки единицы груза от поставщиков к фиктивному потребителю затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. То же самое получаем и в отношении фиктивного поставщика. Прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверить, к какой модели она принадлежит, и только после этого составить таблицу для ее решения.
Как и при решении задачи линейного программирования, симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Число переменных Xij в транспортной задаче с m пунктами отправления и n пунктами назначения равно nm, а число уравнений в системах (2) и (3) равно n+m. Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно n+m-1 отличных от нуля неизвестных. Если в опорном плане число отличных от нуля компонентов равно в точности n+m-1, то план является не выраженным, а если меньше - то выраженным. Для определения опорного плана существует несколько методов. Три из них - метод северно-западного угла, метод минимального элемента и метод аппроксимации Фогеля - рассмотрены ниже. При составлении первоначального опорного плана методом северо-западного угла стоимость перевозки единицы не учитывается, поэтому построенный план далек от оптимального, получение которого связано с большим объемом вычислительных работ. Обычно рассмотренный метод используется при вычислениях с помощью ЭВМ. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической важности этой задачи и специфики ее ограничений [каждое неизвестное входит лишь в два уравнения системы (2) и (3) и коэффициенты при неизвестных равны единице] для определения оптимального плана транспортной задачи разработаны специальные методы. Два из них - метод потенциалов и Венгерский метод - рассматриваются ниже. 7 8 9 10 Метод "северо-западного" угла Шаг 1. Составляют транспортную таблицу. Шаг 2.Транспортную таблицу начинают заполнять с левого верхнего (северо-западного) угла. При заполнении двигаются по строке вправо и по столбцу вниз. В клетку, находящуюся на пересечении первой строки и первого столбца, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос:
|

 = M > 0
= M > 0  .
. = ai,
= ai, = bj.
= bj. ,
,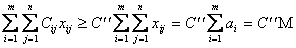
 , называется открытой. Для открытой модели может быть два случая:
, называется открытой. Для открытой модели может быть два случая: ;
; .
. при ограничениях
при ограничениях ,i = 1, 2,..., m, (случай а)
,i = 1, 2,..., m, (случай а) , j = 1, 2,..., n;
, j = 1, 2,..., n;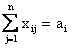 , i = 1, 2,..., m, (случай б)
, i = 1, 2,..., m, (случай б) , j = 1, 2,..., n,
, j = 1, 2,..., n,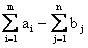 . В случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик Am+1, запасы которого am+1 =
. В случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик Am+1, запасы которого am+1 = 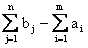 .
. Если а1 < b2, то х11 = a1 и предложение первого поставщика полностью исчерпано. Первая строка вычеркивается, и двигаются по столбцу вниз. В клетку, находящуюся на пересечении первого столбца и второй строки, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: х21 =
Если а1 < b2, то х11 = a1 и предложение первого поставщика полностью исчерпано. Первая строка вычеркивается, и двигаются по столбцу вниз. В клетку, находящуюся на пересечении первого столбца и второй строки, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: х21 =


