Рішення
Нехай
а ={65 80 105} — вектор ресурсів складів А, В, С; b ={45 60 80 65} — вектор потреб споживачів I, II, III, IV Ця транспортна задача є закритою, тому що сумарні ресурси і сумарні потреби збігаються:
Сформулюємо математичну модель задачі. 1. Цільова функція, що відповідає сумарним витратам на перевезення бензину зі складів споживачам, має вигляд
2. При цьому задача має наступні обмеження: обмеження по ресурсах
обмеження по потребах:
умови невід’ємності:
Таким чином, рішення транспортної задачі зводиться до мінімізації цільової функції (8) для усіх величин xij, що задовольняють умовам (9)-(11). Перейдемо до реалізації задачі в Excel, робочий лист якого з усією необхідною інформацією показаний на рис. 1.
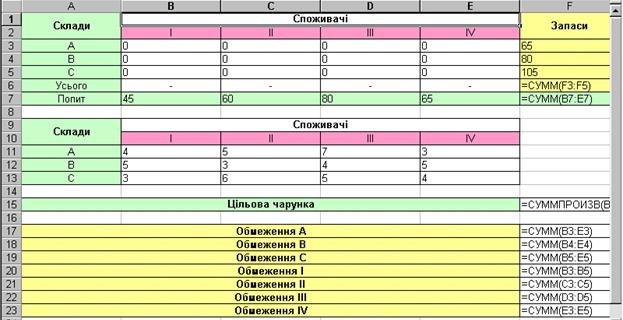
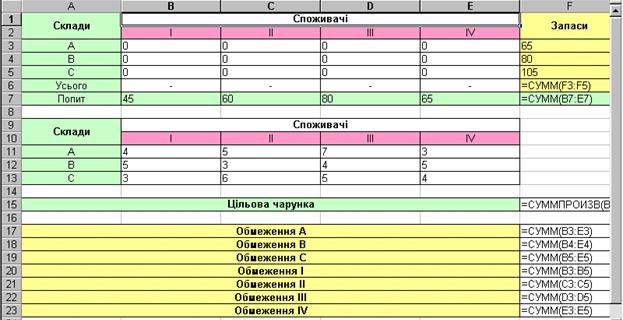
Рис. 1 Початкова таблиця задачі 1
Формується він у такий спосіб — у діапазон осередків В З: Е 5 як початкові значення попереднього розподілу запасів бензину на складах А, B, C між споживачами I, II, III, IV заносимо нулі. У діапазон осередків F 3: F 5 записуємо запаси бензину, розміщені на складах А, B, C відповідно. У діапазон осередків B 7: Е 7 — потреби в бензині споживачів I, II, III, IV. В осередок F 6 заносимо контрольну суму обсягів бензину, розміщеного на складах, тобто суму осередків F 3: F 5. В осередок F 7 заносимо контрольну суму потреби в бензині всіх споживачів, тобто суму осередків B 7: Е 7. Оскільки розглянута модель транспортної задачі закрита, контрольні суми в осередках F 6 і F 7 повинні збігатися. У діапазоні осередків B 11: Е 13 формуємо матрицю вартостей (витрат) перевезень однієї тонни бензину з кожного складу кожному споживачу. Далі в осередок F 15 заносимо формулу для розрахунку цільової функції, використовуючи вбудовану функцію = СУММПРОИЗВ (B 11: Е 13; В З: Е 5). Обмеження задачі записуються в осередки F I7: F 23, куди вводяться функції, що відповідають вираженням лівих частин обмежень (9), (10). Для обмеження А заносимо в осередок F 17 сумарну кількість бензину, що буде перевезено зі складу А всіх споживачів, скориставшись убудованою функцією СУММ. Для обмежень B, C вміст осередку F 17 копіюється в осередки F 18, F 19. Для обмеження I заносимо в осередок F 20 сумарну кількість бензину, що доставляється першому споживачу з усіх складів. Для цього встановлюємо курсор в осередок F 20 і уводимо формулу, що має вигляд = СУММ (В З: B 5). Аналогічно заповнюються осередки F 20: F 23 для обмежень II—IV.
Рис 2. Зміст осередків початкової таблиці задачі 1 А.2. Рішення задачі розподілу ресурсів з використанням моделі “Транспортна задача”. Завершивши побудову робочого листа, запускаємо з меню Сервис команду Поиск решения. З;являється діалогове вікно, наведене на рис. 3.
Рис. 3 Діалогове вікно Поиск решения для задачі 1 В полі Установить целевую ячейку подаємо адрес осередку, який буде містити рішення задачі. В нашому випадку це осередок F 15. В розділі Равной: вибираємо перемикач «минимальному значению», а в полі Изменяя ячейки — діапазон осередків $В$ 3: $Е$ 5, значення в яких можуть змінюватися в процесі пошуку рішення (величини попереднього розподілу запасів бензину зі складів А, В, С між споживачами I, II, III, IV). Для введення обмежень задачі, тиснемо на кнопку Добавить. При цьому відкривається діалогове вікно Добавление ограничения (рис. 4).
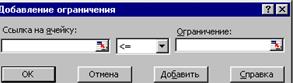
Рис. 4. Діалогове вікно Добавление ограничения для задачі 1 Вводимо перше обмеження: $F$ 17= $F$ 3, тобто сумарна кількість перевезеного зі складу А бензину для всіх споживачів дорівнює запасу бензину, розміщеного на тому ж складі. Так само вводимо інші обмеження задачі: $F$ 18= $F$ 4; $F$ 19= $F$ 5; $F$ 20= $B$ 7; $F$ 21= $C$ 7; $F$ 22= $D$ 7; $F$ 23= $E$ 7, за кожним разом натискуючи після закінчення вводу обмеження кнопку ОК. Для реалізації умови невід’ємності значень (11) в діалоговому вікні Поиск решения натискаємо клавіш Параметры и посля появи ще одного діалогового вікна Параметры поиска решения (рис. 5) включаємо прапорець Неотрицательные значения. Слід відзначити, що умови невід’ємності (11) можна також реалізувати у вигляді обмежень для діапазону осередків В З :Е 5.
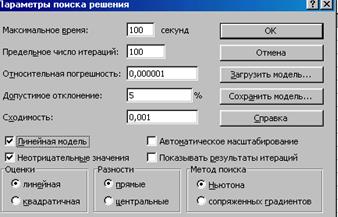
Рис. 5. Параметри пошуку рішення для задачі 1
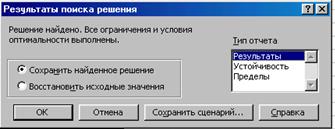
Після натискання кнопки Выполнить діалогового вікна Поиск решения (див. рис. 3) з’являється діалогове вікно Результаты поиска решения (рис. 6). Рис. 6. Вікно Результаты поиска решения При необхідності за його допомогою можна сформувати звіти про хід рішення задачі (або відмовитися від них). Звіти пропонуються трьох типів: Результаты, Устойчивость. Пределы. Можна вибрати одразу декілька типів звіту, виділивши їх за допомогою миша при нажатому клавішу <Ctrl>. Кожний звіт буде створено на окремому рабочому аркуші. В нашому випадку достатньо вибрати тип звіту — Результаты. Після натискання кнопки ОК з’являється новий робочий аркуш із звітом за результатами, а на робочому аркуші початкова таблиця набуває вигляду, показаного на рис. 7
Рис. 7. Робочий лист Excel із результатами рішення задачі 1
|

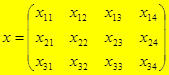 – матриця, що визначає план перевезень;
– матриця, що визначає план перевезень; – матриця транспортних витрат;
– матриця транспортних витрат;
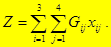 (8)
(8)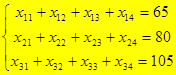 (9)
(9) (10)
(10)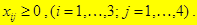 (11)
(11)
 Результат представлений на рис. 2.
Результат представлений на рис. 2.