Задача 2. На трьох складах А, В, С є 65, 100 й 105 комплектів озброєння відповідно
На трьох складах А, В, С є 65, 100 й 105 комплектів озброєння відповідно. Необхідно скласти такий план перевезення 45, 60, 80 й 65 комплектів озброєння в чотири частини (чотирьом споживачам) I, II, III, IV відповідно, щоб сумарні витрати на це були мінімальними. Вартість перевезення одного комплекту озброєння (в гривнах) зі складів до частин вказана в таблиці:
Рішення Через те, що в цій транспортній задачі сумарні ресурси перевищують сумарні потреби, її треба вважати відкритою:
Уводимо фіктивного споживача V з потребою
а також вартості перевезення зі складів А, В, С до фіктивного споживача V: G 15=0; G 25=0; G 35=0, позначивши через х 15; х 25; х 35 кількості перевезених комплектів відповідно зі складів А, В, С частині V. Після таких дій відкрита модель транспортної задачі перетворилася в закриту модель, тому що
Тепер
а={65 100 105}— вектор ресурсів складів А, В, С; b={45 60 80 65 20} — вектор потреб споживачів I, II, III, IV, V.
Сформулюємо математичну модель задачі. 1. Цільова функція, що відповідає сумарним витратам на перевезення комплектів озброєння зі складів частинам, має вигляд
2. При цьому обмеження будуть наступними: обмеження по ресурсах:
обмеження по потребах:
умови невід’ємності:
умови цілочисленості:
Таким чином, рішення транспортної задачі зводиться до мінімізації цільової функції (12) для усіх величин xij, що задовольняють умовам (13)–(16). Вихідна таблиця, що містить усю необхідну для рішення задачі інформацію, подана на рис.8.
Рис. 8. Початкова таблиця задачі 2
|





 – матриця, що визначає план перевезень;
– матриця, що визначає план перевезень; – матриця транспортних витрат;
– матриця транспортних витрат;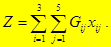 (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)



