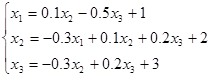Случай, когда матрица А близка к единичной.

Если после вычитания из диагональных элементов по 1 сумма модулей элементов всех строк (столбцов) матрицы А будет меньше 1, то систему легко свести к нужному в методе простых итераций виду, выделяя из i- го уравнения x _i и перенося его в левую часть.

Этот случай похож на предыдущий, но обязательно ли матрица, близкая к единичной является матрицей с диагональным преобладанием?.

Упражнение 9.6. Выяснить, бывают ли системы линейных уравнений без диагонального преобладания, но с матрицей А, близкой к единичной.

Пример2.

ó

Заметим, что в некоторых случаях удобнее комбинировать оба способа преобразования уравнений исходной системы – деление на диагональные элементы и вычитание из них 1.

Упражнение 9.7 Для матриц из примеров 1 и 2 посчитать их нормы в трех различных метриках пространства Rⁿ и найти минимальную (число q).

Упражнение 9.8. Для системы из примера1, приведенной к нужному виду, взять в качестве Х₀ нулевой вектор и построить два следующих вектора итерационной последовательности.

Напомним, что метод простых итераций, также как и другие итерационные методы решения систем линейных уравнений, обычно применяют, если порядок системы велик, например сотни или тысячи уравнений, и применение любых прямых методов затруднено в связи с очень большим количеством вычислений.

Контрольные вопросы.

1. К какому виду преобразуют исходную систему для применения метода итераций?

2. Следствием какого общего метода является рассматриваемый метод?

3. Какие еще похожие методы встречались в пройденной части курса?

4. В чем преимущество метода итераций перед другими методами?

5. В каких случаях стремятся применять метод простых итераций?

6. Каковы условия применимости данного метода?

7. В чем суть метода?

8. Какова скорость сходимости последовательности векторов к решению?

9. Сформулируйте условие окончания вычислений в методе простых итераций?

10. Какие простые случаи сведения системы к нужному в методе итераций виду Вы знаете?

Содержание лабораторной работы.

6. Ответить на вопросы контролирующей программы.

7. Составить, отладить и протестировать на контрольных примерах программу решения систем линейных уравнений методом простых итераций.

8. Попробовать применить программу к системам, где метод простых итераций не применим. Дополнить программу проверкой применимости метода.

9. Составить отчет, содержащий цель и назначение работы, постановку задачи, текст программы и варианты исполнения для своих данных.