Постановка задачи.
Пусть  -функция, определенная на некотором множестве
-функция, определенная на некотором множестве 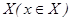 . Будем рассматривать задачу минимизации функции
. Будем рассматривать задачу минимизации функции  . Любая задача максимизации функции
. Любая задача максимизации функции  на
на  равносильна задаче минимизации функции
равносильна задаче минимизации функции  на том же множестве
на том же множестве  . Поэтому можно ограничиться лишь изучением задач минимизации.
. Поэтому можно ограничиться лишь изучением задач минимизации.
Классический подход.
Пусть  кусочно-непрерывная и кусочно-гладкая функция на отрезке [a, b] ([a, b]ÎX). Это значит, что на [a, b] может существовать лишь конечное число точек, в которых функция
кусочно-непрерывная и кусочно-гладкая функция на отрезке [a, b] ([a, b]ÎX). Это значит, что на [a, b] может существовать лишь конечное число точек, в которых функция  либо терпит разрыв первого рода, либо непрерывна, но не имеет производной. Тогда точками экстремума функции
либо терпит разрыв первого рода, либо непрерывна, но не имеет производной. Тогда точками экстремума функции  на [a, b] могут быть лишь те точки, в которых выполняется одно из следующих условий: 1)
на [a, b] могут быть лишь те точки, в которых выполняется одно из следующих условий: 1)  терпит разрыв; 2)
терпит разрыв; 2)  непрерывна, но производная не существует; 3)производная
непрерывна, но производная не существует; 3)производная  существует и равна нулю; 4)
существует и равна нулю; 4)  или
или  . Такие точки принято называть точками подозрительными на экстремум. Поиск точек экстремума функции начинают с нахождения всех точек, подозрительных на экстремум. После того, как такие точки найдены, проводят дополнительное исследование и отбирают среди них те, которые являются точками локального минимума (максимума).
. Такие точки принято называть точками подозрительными на экстремум. Поиск точек экстремума функции начинают с нахождения всех точек, подозрительных на экстремум. После того, как такие точки найдены, проводят дополнительное исследование и отбирают среди них те, которые являются точками локального минимума (максимума).
Упражнение 1. Запишите достаточное условие того, что подозрительная точка x* Î [a, b] является точкой локального минимума (максимума).
Чтобы найти глобальный минимум (максимум) функции  на [a, b], нужно перебрать все точки локального минимума (максимума) на [a, b] и среди них выбрать точку с наименьшим (наибольшим) значением функции, если таковая существует (если вместо [a, b] имеем дело с R, то следует изучить поведение функции при
на [a, b], нужно перебрать все точки локального минимума (максимума) на [a, b] и среди них выбрать точку с наименьшим (наибольшим) значением функции, если таковая существует (если вместо [a, b] имеем дело с R, то следует изучить поведение функции при  или
или  ).
).
К сожалению, классический метод имеет весьма ограниченное применение. В практических задачах вычисление  зачастую является непростым делом. Например, значения функции
зачастую является непростым делом. Например, значения функции  определяется из наблюдений или эксперимента, и получить информацию о её производной крайне трудно. Поэтому важно иметь также и другие методы поиска экстремума, не требующие вычисления производной, удобные для реализации на ЭВМ.
определяется из наблюдений или эксперимента, и получить информацию о её производной крайне трудно. Поэтому важно иметь также и другие методы поиска экстремума, не требующие вычисления производной, удобные для реализации на ЭВМ.
Упражнение 2. Найти точки экстремума функции  = sin3(x) + cos3(x) на отрезках [0, 3p/4], [0, 2p].
= sin3(x) + cos3(x) на отрезках [0, 3p/4], [0, 2p].
Упражнение 3. Пусть  = (1 + e1/x )-1 при x¹0, f(0)=0. Найти точки экстремума этой на отрезках [-1, 0], [-1, 1], [1, 2] и на R.
= (1 + e1/x )-1 при x¹0, f(0)=0. Найти точки экстремума этой на отрезках [-1, 0], [-1, 1], [1, 2] и на R.
Поиск экстремумов функций одной переменной является самостоятельной и часто встречаемой задачей. Кроме того, к нему сводится более сложная задача поиска экстремумов функций множества переменных.

 -функция, определенная на некотором множестве
-функция, определенная на некотором множестве 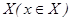 . Будем рассматривать задачу минимизации функции
. Будем рассматривать задачу минимизации функции  равносильна задаче минимизации функции
равносильна задаче минимизации функции  на том же множестве
на том же множестве  существует и равна нулю; 4)
существует и равна нулю; 4)  или
или  . Такие точки принято называть точками подозрительными на экстремум. Поиск точек экстремума функции начинают с нахождения всех точек, подозрительных на экстремум. После того, как такие точки найдены, проводят дополнительное исследование и отбирают среди них те, которые являются точками локального минимума (максимума).
. Такие точки принято называть точками подозрительными на экстремум. Поиск точек экстремума функции начинают с нахождения всех точек, подозрительных на экстремум. После того, как такие точки найдены, проводят дополнительное исследование и отбирают среди них те, которые являются точками локального минимума (максимума). или
или  ).
).


