ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ ПО ПРОЕКТИРОВАНИЮ БАЛОК С ГИБКОЙ СТЕНКОЙ
18.1*. Для разрезных балок с гибкой стенкой симметричного двутаврового сечения, несущих статическую нагрузку и изгибаемых в плоскости стенки, следует, как правило, применять стали с пределом текучести до 430 МПа (4400 кгс/см2).
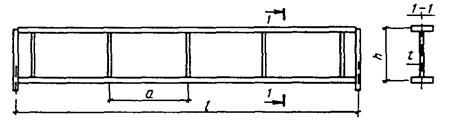
Рис. 22. Схема балки с гибкой стенкой 18.2*. Прочность разрезных балок симметричного двутаврового сечения, несущих статическую нагрузку, изгибаемых в плоскости стенки, укрепленной только поперечными ребрами жесткости (рис. 22), с условной гибкостью стенки 6 ≤ (M / Mu)4 + (Q / Qu)4 ≤ 1, (158) где М и Q - значения момента и поперечной силы в рассматриваемом сечении балки; Мu - предельное значение момента, вычисляемое по формуле Qu - предельное значение поперечной силы, вычисляемое по формуле В формулах (159) и (160) обозначено: t и h - толщина и высота стенки; Af - площадь сечения пояса балки; τcr и μ; - критическое напряжение и отношение размеров отсека стенки, определяемые в соответствии с п. 7.4*; β; - коэффициент, вычисляемый по формулам: при α; ≤ 0,03 β; = 0,05 + 5α ≥ 0,15; (161) при 0,03 < α; ≤ 0,1 β; = 0,11 + 3 α; ≤ 0,40. (162) Здесь где Wmin - минимальный момент сопротивления таврового сечения, состоящего из сжатого пояса балки и примыкающего к нему участка стенки высотой 0,5t а - шаг ребер жесткости. 18.3. Поперечные ребра жесткости, сечение которых следует принимать не менее указанных в п. 7.10, должны быть рассчитаны на устойчивость как стержни, сжатые силой N, определяемой по формуле где все обозначения следует принимать по п. 18.2*. Значение N следует принимать не менее сосредоточенной нагрузки, расположенной над ребром. Расчетную длину стержня следует принимать равной lef = h (1 - β;), но не менее 0,7 h. Симметричное двустороннее ребро следует рассчитывать на центральное сжатие, одностороннее - на внецентренное сжатие с эксцентриситетом, равным расстоянию от оси стенки до центра тяжести расчетного сечения стержня. В расчетное сечение стержня следует включать сечение ребра жесткости и полосы стенки шириной 0,65 t 18.4. Участок стенки балки над опорой следует укреплять двусторонним опорным ребром жесткости и рассчитывать его согласно требованиям п. 7.12. На расстоянии не менее ширины ребра и не более 1,3 t 18.5. Устойчивость балок не следует проверять при выполнении требования п. 5.16*, а настоящих норм либо при расчетной длине lef ≤ 0,21 bf 18.6. Отношение ширины свеса сжатого пояса к его толщине должно быть не более 0,38 18.7*. Местное напряжение σloc в стенке балки, определяемое по формуле (31), должно быть не более 0,75 Ry, при этом значение lef следует вычислять по формуле (146). 18.8*. При определении прогиба балок момент инерции поперечного сечения брутто балки следует уменьшать умножением на коэффициент α; = 1,2 - 0,033 18.9*. В балках по п. 18.1* с условной гибкостью стенки 7 ≤ Прочность таких балок следует проверять по формуле где δ; - коэффициент, учитывающий влияние поперечной силы на несущую способность балки и определяемый по формуле δ = 1- 5,6 Afh / (Awl). При этом следует принимать tf ≥ 0,3
|

 ≤ 13 следует проверять по формуле
≤ 13 следует проверять по формуле ; (159)
; (159)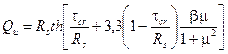 . (160)
. (160)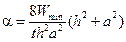 ,
,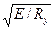 (относительно собственной оси тавра, параллельной поясу балки);
(относительно собственной оси тавра, параллельной поясу балки);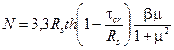 , (163)
, (163) , (163, а)
, (163, а)


