Практическое использование моделей строения.
Моделирование строение заключается в описании закономерного распределения числа деревьев в древостое по различным таксационным показателям теми или иным уравнениями, называемые моделями. Вопросы моделирования в общем виде студенты, обучающиеся по специальности «Лесное хозяйство», изучали в курсах «системный анализ» и «биометрия». Здесь мы рассмотрим моделирование в приложении к лесу, а конкретнее к лесам Беларуси. Напомним краткое определение модели. Модель – это мысленно представляемая или материально реализуемая система, которая отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает нам новую информацию об этом объекте. Это определение предлагают использовать К.Е. Никитин и А.З. Швиденко. Есть и другие определения модели. В принципе, графическое воспроизведение закономерностей распределения деревьев, показанное выше, тоже является моделью только графической. В докомпьютерную эпоху часто именно такими моделями и ограничивались из-за сложностей вычислений по уравнениям. В настоящее время в основном используют математические модели. Правда, графическое отражение этих уравнений остается важным в исследованиях, т.к. позволяют наглядно увидеть изучаемые закономерности. Дело облегчается тем, что графики выдает компьютер. Модель кривой нормального распределния имеет вид
где: f(x) – функция плотности нормального распределения
xi – переменная величина
Из уравнения 10.1 следует, что нормальное распределение характеризуется 2 параметрами. При этом предполагается, что асимметрия и эксцесс равны нулю или очень близки к нему. Выше показано, что равенство нулю
где
Уравнение (10.2) представляет собой бесконечный ряд с повышающимся уровнем производных f(x). Для практического использования имеют существенное значение три первые члена уравнения, приведенные в (10.2). При моделировании строения древостоев, начиная от молодняков до спелых и переспелых насаждений, нельзя ограничиваться лишь уравнениями (10.1 и 10.2), особенно при описании молодняков. С увеличением возраста и диаметра ряд становится более пологим (рисунок 10.4). На этом рисунке наглядно видно, что с увеличением среднего диаметра ряд становится более «нормальным». Из этогоже рисунка видно, что ряды в самом молодом возрасте при небольшом среднем диаметре отличаются от характера распределения в более старшем возрасте при больших велчинах средних диаметров. Исследования многих учёных (А.Г.Мошкалев, А.З.Швиденко,. В.С.Моисеев, В.Ф.Багинский) показали, что лишь с 30-50 лет древостои могут быть охарактеризованы кривой типа А. Ещё большую неопределенность в ряде случаев внесят рубки промежуточного пользования, особенно при их неоднозначном проведении.
Рисунок 10.4 Изменение строения древостоев при увеличении среднего диаметра от 4 до 12см (по В. В. Антанайтису).
Из курса биометрии известно, что для описания рядов имеются общие подходы, основанные на применении кривых Пирсона и Джонсона. В лесохозяйственной литературе нашёл применение первый подход, т.е. использование свойства кривых Пирсона. В частности, распределение в естественных молодняках часто описывают кривой 1 типа Пирсона. Применяя систему кривых Пирсона, исследователь не связывает себя ни с какой предварительной гипотезой, например, о нормальности распределения. Тип кривой выбирается по критерию Пирсона (
где r3 и r4 соотвественно 3 и 4 основные моменты. Выбор типа кривой проводится по специальным таблицам, имеющимся в учебникам по биометрии. Вычисление кривых Пирсона весьма сложны, что сдерживало их применение ранее. Теперь есть компьютерные программы, по которым такие вычисления провести легко. Одним из перспективных направлений при моделировании строения является установление закономерных связей статистик с таксационными показателями древостоя: Д, Н, П, А и т.д. К.Е. Никитин, изучая строение древостоев лиственницы на Украине, не обнаружил связи асимметрии и эксцесса с возрастом и средним диаметром. Более поздние исследования С.А. Дыренкова, А.Г. Мошкалева, В.Ф. Багинского показали, что такая зависимость существует. Поэтому, разработав многомерные регрессионные модели, где аргументами будут возраст, средний диаметр, полнота, густота и т.д., мы можем установить величину При дифференцировании насаждений по породам и бонитетам прогнозирование статистик рядов распределения существенно улучшается. В этом случае многомерная корреляции асимметрии с таксационными показателями выражается коэффициентами множественной корреляции от 0.6 до 0.85, а Е находится лишь в пределах 0.2-0.3. В условиях интенсивного хозяйства на величину статистик существенно влияют рубки ухода. Учитывая это обстоятельство, В.Ф. Багинским разработана типизация строения древостоев. Введение в уравнение множественной регрессии аргумента «тип строения» повышает прогностические возможности модели на 30-40%, а по Е на 50-60%, делая нахождение статистик достоверным на уровне 90-95%. Типы строения разработаны в зависимости от силы и направленности рубок промежуточного пользования. Типизация строения древостоев сводится к выделению 6 типов. 1.Нормальный лес-строение нормальное или несколько асимметричное (0 < а < 0,2; Е * 0 ± 0,1). Аппроксимация кривой Гаусса-Лапласа, иногда Грама-Шарлье. 2. Слабые рубки ухода низовым методом. Среднее значение ( 3. Средние и сильные рубки промежуточного пользования низовым методом. Асимметрия возрастает до 0,5-1,1, эксцесс колеблется от +0,1-0,6 до -0,4 в зависимости от схемы рубок. Для аппроксимации необходимо применять кривую I Пирсона. 4. Слабые рубки ухода верховым методом. Статистики ряда (а, Е, а) изменяются аналогично типу 2. Среднее значение уменьшается. 5. Средние и сильные рубки промежуточного пользования верховым методом. Среднее значение уменьшается на 20-25%, асимметрия отрицательная (от -0,4 до -1,2). Эксцесс доходит до 1 в зависимости от схемы вырубки. Аппроксимация кривой I Пирсона. 6. Беспорядочные выборочные рубки. В этом случае изменение характеристик ряда не имеет какой-либо четкой закономерности и может идти по схемам, соответствующим типам 2-5. Нередко в этом случае воздействие на древостой бывает разнохарактерным, и ряд остается в пределах кривой Грама-Шарлье. Но прогнозировать конкретные числовые характеристики ряда здесь затруднительно, и их следует вычислять по данным сплошных перечетов, используя для аппроксимации семейство кривых Пирсона (в основном достаточно и кривой типа I). Типизация строения позволяет точнее выявить закономерности строения древостоев и дает возможность лучше осуществлять расчет и прогноз товарной структуры древостоев при интенсивном ведении лесного хозяйства. Для лесов Беларуси В.Ф. Багинским на основе анализа свыше 900 пробных площадей выведены усредненные ряды распределения числа стволов по диаметру. Ряды дифференцированы по породам и описывают строение приспевающих, спелых и перестойных древостоев. Выравнивание опытного материала сделано с помощью уравнения кривой обобщенного нормального распределения – тип А или Грама – Шарлье. Конкретные ряды для древостоев в Беларуси показаны в таблице 10.13. Статистики рядов,показанных в таблице 10.13 приведены в таблице 10.14.
Таблица 10.13 Ряды распределения числа стволов по диаметру по относительным ступеням толщины в лесах Беларуси
Таблица 10.14 Статистики рядов распределения числа стволов по толщине
Анализ таблиц 10.13 и 10.14 и сопоставление их с известными закономерностями А. В. Тюрина и Н.В.Третьякова и других авторов прошлого, которые описаны выше, показало, что в древостоях Беларуси имеются больший размах ряда распределения (особенно для ели и дуба), значительно меньшая концентрация деревьев в средних ступенях толщины, ранг среднего дерева сдвинут ближе к середине ряда. Это еще раз свидетельствует о необходимости учитывать местные особенности роста и ведения хозяйства, оказывающего влияние на строение древостоев.
Практическое значение рядов распределение деревьев в насаждениях по таксационным показателям состоит в разработке на их основе методов товаризации древостоев. О возможности составлять объемные и сортиментные таблицы по средней формы стволов, что установлено Ф.П. Моисеенко и В.Х. Захаровым, сказано выше. Решающее значение имеет значение законов распределения при составлении товарных таблиц, где выход сортиментов определяют в зависимости от средних диаметра и высоты. Закономерности строения используют и при проведении материально-деленной оценки с использованием выборочно-измерительных методов. Для описания ряда в этом случае применяют различные модели; нормальную кривую, уравнение Грама-Шарлье, систему кривых Пирсона и т д. О.А. Атрощенко рекомендует для описания рядов
Обобщая вышеизложенное в настоящей главе, можно сделать следующие выводы 1. Распределение числа деревьев по основным таксационным показателям носит закономерный характер. Для средневозрастных древостоев и старше оно может быть описано кривой нормального распределения или обобщенного нормального распределения (тип А),допустимо использовать здесь и 2. Ранг среднего дерева в древостоях Беларуси колеблется в пределах 54-58%. 3. Ряды распределения в естественных молодняках обычно не соответствуют кривой нормального распределения. Здесь рекомендуется использовать систему кривых Пирсона, чаще всего типа I. 4. Изменчивость диаметров в древостое колеблется от 50-60% в естественных молодняках до 22-25% в спелом лесу. Это значит, что при закладке пробных площадей в молодняках в возрасте 8-12 лет необходимо наличие на пробе 400-500 деревьев, а в спелом лесу достаточно иметь на пробе 200 деревьев. Для определения средней высоты с приемлемой точностью достаточно измерить 12-20 деревьев в зависимости от возраста. 5. Малая изменчивость формы ствола, выраженная через f и q2, и нормальное распределение этих показателей в древостое, стали теоретической основой составления объемных таблиц по средней формы ствола. 6. На строение древостоя оказывают влияние рубки ухода. По показателям силы и направленности рубок ухода в Беларуси разработана типизация строения, которая включает 6 типов. 7. Практическое значение закономерностей строения заключается в их применении для разработки методов таксации и особенно товаризации насаждений, т.е при составлении сортиментных и товарных таблиц.
|

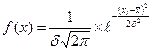 ,(10.1)
,(10.1) - среднее значение
- среднее значение - среднеквадратичное отклонение
- среднеквадратичное отклонение - 2,1416
- 2,1416 - 2,71828
- 2,71828 и Е при исследовании рядов в реальных древостоях Беларуси представляет собой, скорее, исключение, чем правило. Более адекватно ряды описываются уравнениями, где в качестве аргументов присутствуют асимметрия и эксцесс. Такой кривой является кривая типа А, называемая кривой обобщенного нормального распределения или Грамма-Шарлье, включающая 4 параметра. Ее уравнение имеет вид
и Е при исследовании рядов в реальных древостоях Беларуси представляет собой, скорее, исключение, чем правило. Более адекватно ряды описываются уравнениями, где в качестве аргументов присутствуют асимметрия и эксцесс. Такой кривой является кривая типа А, называемая кривой обобщенного нормального распределения или Грамма-Шарлье, включающая 4 параметра. Ее уравнение имеет вид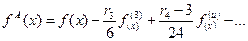 (10.2)
(10.2) - плотность обобщенного нормального распределения
- плотность обобщенного нормального распределения

 - соответственно третья и четвертая производная f(x).
- соответственно третья и четвертая производная f(x).
 ).
). (10.3)
(10.3) и Е для интересующих нас древостоев.Это позволяет легко подобрать тип кривой, которая адекватно описывает исследуемые ряды. При этом прогнозирование рядов распределения по моделям связи,
и Е для интересующих нас древостоев.Это позволяет легко подобрать тип кривой, которая адекватно описывает исследуемые ряды. При этом прогнозирование рядов распределения по моделям связи,  ) увеличивается незначительно. Строение нормальное или слегка асимметричное (0 < а < 0,3; Е от -0.03 до -0,23). Ряд сужается. Аппроксимация типов строения 1-2 проводится с помощью кривой обощенного нормального распределения (типа А).
) увеличивается незначительно. Строение нормальное или слегка асимметричное (0 < а < 0,3; Е от -0.03 до -0,23). Ряд сужается. Аппроксимация типов строения 1-2 проводится с помощью кривой обощенного нормального распределения (типа А).

 -функцию, которая тоже хорошо отражает ряды распределения в лесах Беларуси. Подробное описаниее выборочных методов товаризации сделано ниже.
-функцию, которая тоже хорошо отражает ряды распределения в лесах Беларуси. Подробное описаниее выборочных методов товаризации сделано ниже.


