Определение суммы площадей поперечных сечений и среднего диаметра методом Биттерлиха
В. Биттерлих для упрощенного определения сумм площадей сечений предложил прибор die Winkelzahlprobe, который получил название прибора Биттерлиха. Описание этого прибора сделано выше, когда шла речь о приборах, применяемых в лесной таксации. Сущность применения прибора Биттерлиха заключается в следующем. Если наблюдатель, поворачиваясь на месте, прибором Биттерлиха опишет на местности круг, то диаметр этого круга будет 2м, а радиус 1м (рисунок 11.2). Площадь такого круга равна По отношению к площади описанного круга радиусом 1м сумма площадей поперечных сечений трех деревьев диаметром 2см каждое составляет
Рисунок 11.2 Визирование прибором В.Биттерлиха при круговой площади радиусом в 1м
Следовательно, площадь поперечного сечения каждого дерева равняется 0003: 3 = 0,0001 круговой пробной площади. Если поперечные сечения имеющихся на пробной площадке деревьев составляют 0,0001 ее части, то на 1 га древостоя, состоящего из таких же деревьев, они будут равны 1м2, так как 0,0001 от площади 1га, или 10000 м2, это составляет 1м2. Предположим, что в двух метрах от наблюдателя находится дерево диаметром 4см. Визируя на это дерево прибором Биттерлиха, мы увидим, то оно полностью закроет 2-сантиметровую рамку прибора Биттерлиха. Площадь поперечного сечения этого дерева равна π22 =π4. Если из точки визирования описать круг радиусом 2 м, то его площадь будет равна π2002 =π40 000. Отношение площади поперечного сечения дерева диаметром 4 см к площади круга радиусом 2 м в данном случае составляет
Следовательно, и в данном случае на 1 га площадь поперечных сечений аналогичных деревьев будет 1 м2. Рассмотренные нами примеры позволяют заключить, что при пользовании прибором Биттерлиха дерево, полностью закрывающее предметную рамку диоптра при учете сумм площадей поперечных сечений на 1га, можно приравнять к 1м2 поперечного сечения при коэффициенте полнотомера (его еще называют коэффициентом Биттерлиха) q = 1,. Если таксатор, визируя вокруг себя деревья, найдет 20 деревьев, перекрывающих прицельную рамку, то это означает, что в данном древостое на 1га сумма площадей сечений равна 20м2. Деревья каждой отдельной ступени толщины могут войти в число учитываемых только в той круговой пробе, диаметр которой равен такому числу метров, сколько сантиметров содержится в данной ступени толщины. Например, деревья толщиной 8см будут учитываться на круговой пробе диаметром 8 м, а толщиной 12см - на круговой пробе диаметром 12м. Радиусы и диаметры круговых проб, на которых при таксации с помощью прибора Биттерлиха учитываются деревья отдельных ступеней толщины, показаны на рис. 11.3.На основании изложенного и рисунка. 11.3 можно заключить, что диметры деревьев всех размеров относятся к радиусам круговых пробных площадей как 1:50, а к диаметрам как 1:100.
Рисунок 11.3 Измерение полнотомером суммы площадей сечений древостоя
Толщина деревьев, точно вписывающихся в угол визирования прибора Биттерлиха, увеличенная в 50 раз, указывает расстояние до этих деревьев от глаза наблюдателя. Соответственно такому соотношению диаметров отношение площади поперечных сечений учитываемых деревьев к площади круговых проб будет следующим: . В аналогичном соотношении, т. е. 1:10 000, находится площадь 1м2 с числом квадратных метров, содержащихся в 1га. Этим постоянным, в обоих случаях одинаковым соотношением между поперечным сечением учитываемого дерева и площадью круговой пробы, с одной стороны, и 1м2 Чтобы перейти от относительных значений к абсолютным, числитель полученной дроби надо рассматривать как сумму площадей сечений деревьев, выражаемую в квадратных метрах, а знаменатель -как число квадратных метров в 1га. Ограничивающий угол, или угол визирования прибора, обозначим α, точно вписывающийся в этот угол диаметр дерева - d. Диаметр круговой площадки, на которой учитываются деревья данного размера, равен D, а радиус круговой площадки – r. При этих условиях D= 2r. Толщина ствола с диаметром круговой площадки находятся в следующем соотношении:
Отношение площади поперечного сечения ствола к площади круговой площадки, или ограничивающего круга, для дерева данного диаметра будет
Площадь поперечного сечения (м2) по отношению к площади 1га (м2/га) составляет
Если внутри ограничивающего круга деревьев данного диаметра насчитано N стволов, то сумма площадей поперечных сечений (м2/га) равняется
Уравнение (11.5) в теории В. Биттерлиха является основным. Выражение Например, если ширина предметной рамки 2 см и длина визирного бруска 100 см, угол визирования α = 1˚10’. Половина этого угла имеет sin35' = 0,01, а sin235' *= 0,0001. Соответственно этому множитель При измерении суммы площадей сечений древостоя на реласкопической круговой пробной площадке полнотомером Биттерлиха могут встретиться три варианта учёта деревьев (рисунок 11.3). -- Если диаметр (толщина) дерева полностью перекрывает прицел полнотомера, то принимают G=1 м2; -- -- Если диаметр дерева совпадает с прицелом, то G = 0,5м2; --При диаметре меньше прицела дерево не учитывается. Метод Биттерлиха по существу является выборочным. Поэтому встает вопрос, как определить количество площадок на 1га и места для закладки круговых площадок, т. е. схему выборки. Места закладки круговых проб следует выбирать механически, не прибегая к нахождению более густых или редких куртин леса. За конечную сумму площадей поперечных сечений деревьев, имеющихся на 1га, следует принимать среднеарифметический результат, находимый из всех заложенных круговых пробных площадей Размер КПП можно определить по формуле
где R - радиус КПП; d. - диаметр дерева; А - единица площади;q – коэффициент полнотомера. Примеры: q = 1 (G = 1 м2); q = 2 (1 дерево G = 2 м2); A = 10 000 м2;
d=20см; d=20см; R=10м; R≈7м. Коэффициент Биттерлиха у полнотомера (q) может быть равен 1, 2, 4м2 в зависимости от среднего диаметра древостоя и относительной полноты насаждения. В насаждениях без подроста, имеющих полноту 0,7 = 1,0, применяют коэффициент q = 1. В редких древостоях, где полнота не превышает 0,5-0,6, его принимают равным q = 2, а в насаждениях с подростом q = 4. Ходовые линии - направления, по которым надлежит размещать круговые площадки, - намечаются с учетом конфигурации таксируемого участка. Ходовые линии должны быть параллельны. По ходовой линии круговые площадки закладывают через каждые 20-30 м (рисунок 11.4).Если участок прямоугольной формы, ходовые линии надо прокладывать перпендикулярно длинным сторонам участков. В.С. Чуенков пришел к выводу, что число реласкопических проб на выделе должно составлять
где F - площадь таксируемого участка, га.
На основании этой формулы можно построить сетку квадратов в масштабе лесоустроительного планшета или плана лесонасаждений (рисунок 11.4).
Рисунок 11.4 Схема квадратов для закладки РКПП
На практике широко используются систематическая выборка, например, по диагонали на выделе через равные расстояния закладываются круговые реласкопические площадки Исследования, проведенные во французских приморских сосновых лесах, показали, что на 1 га надо закладывать 4-5 круговых площадок, С увеличением площади участка число круговых площадок на 1 га может быть несколько уменьшено. На выделе площадью 10 га вместо 40 круговых площадок можно ограничиться 30. На участках с незначительной площадью должно быть заложено не менее 5 круговых площадок. При одной или двух круговых площадках ошибки в определении сумм площадей сечений достигают 20%. При подсчете числа деревьев на круговых площадках следует иметь в виду, что одно дерево может заслонять другое. Чтобы избежать этого, подсчет надо начинать с самого толстого дерева, расположенного ближе всех к таксатору. Деревья, очертания которых как бы «касаются» линий угла, следует считать два за одно. Число деревьев, оказавшееся на каждой круговой площадке, записывают в соответствующий учетный бланк. На каждой круговой площадке измеряют диаметры на высоте груди у двух-трех произвольно взятых деревьев. Опыт показал, что этого числа деревьев вполне достаточно для точного определения среднего диаметра. Метод Биттерлиха позволяет весьма просто определить число деревьев на 1га:
G - сумма площадей поперечных сечений деревьев на 1 га, найденная по результатам учета деревьев на круговых площадках; gcp- площадь сечения среднего дерева. При холмистом рельефе полученный результат необходимо разделить на косинус угла наклона местности. Если таксируемый древостой имеет смешанный состав, то каждая древесная порода подлежит отдельному учёту. Допустим, что при первом обороте по кругу мы учитывали вокруг себя только сосновые деревья, причем их оказалось 15. Это означает, что сумма площадей поперечных сечений всей сосны на 1га данного древостоя равна 15м2. Находясь в этой же точке, мы визируем вокруг себя на деревья березы. В результате находим 10 деревьев березы с частичным сдвигом при рассматривании их в призму. Это число указывает на то, что сумма площадей поперечных сечений всех стволов березы, имеющихся на 1 га, равна 10м2.Следовательно, общая сумма площадей поперечных сечений всех деревьев, имеющихся на 1га, будет 15 + 10 = 25м2. Состав таксируемого смешанного древостоя определяется следующим расчетом для сосны для березы В итоге формула состава выразится как 6С4Б. Рассмотрим способ определения среднего диаметра древостоя на выделе с применением углового шаблона (прибора) Биттерлиха. Для начала с помощью углового шаблона находим сумму площадей сечения на 1га. У деревьев, попавших в учёт, измеряют диаметры на высоте 1,3м.Дальнейшие вычисления проводят по схеме, приведенной в таблице 11.5. В нашем примере сумма площадей сечений древостоя G = 28 м2/га, число деревьев N = 873. Средняя площадь сечения
Таблица 11.5 Схема вычисления среднего диаметра
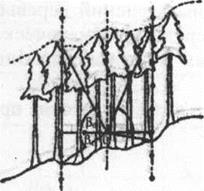
. Коэффициент варьирования диаметров в приспевающих и спелых древостоях равен 20=25%. При измерении 28 деревьев, как показано в таблице11.5, ошибка в определении среднего диаметра составит (вычисления ведем по формуле Профессор Токийского университета Т. Хирата, развивая идею В. Биттерлиха об угловых пробах, разработал оригинальный способ определения средней гармонической высоты древостоя, получивший в таксационной литературе широкую известность. Опубликованная им работа носит название «Вертикальные угловые пробы». Новизна предложения Т. Хирата прежде всего состоит в том, что закладку угловой пробы из горизонтальной плоскости он перенес в вертикальную. В конечном итоге угловая проба, закладываемая по способу Т. Хирата, представляет собой конус, перевернутый вершиной вниз, (рисунок 11.5) Основание этого конуса находится вверху на уровне вершин деревьев, имеющих средние высоты.
Рисунок 11.5 Высота Хирата Сущность этого способа такова. Допустим, что таксируемый участок имеет горизонтальную поверхность. Таксатор находится в точке О (в центре круговой площади) и через просвет прицела визирует на дерево, имеющее высоту hi,. Рассматриваемое дерево относится к категории деревьев i. Радиус закладываемой таким путем круговой пробы равен Ri. На круговой пробе i площадью, равной πR2i, м2, оказывается ti деревьев категории i, закрывающих просвет прицела. Для площади древостоя в 1га рассматриваемая величина будет равна
Для всей категории высот hi, сумма деревьев составляет Если число деревьев на гектаре обозначить через N,то средняя площадь круга будет составлять
откуда
Если β = 60˚34’, то
Угол визирования β при закладке круговой пробы строится не по поверхности земли, а на высоте (h) от земли. Поэтому
t – количество деревьев, попавших в учет, т.е. в угол визирования; На основе открытия Биттерлиха можно непосредственно в лесу определить запас древостоя. В 1961г. В. М. Иванюта предложил метод «десятичных пробных площадей», в основе которого лежит теория угловых измерений и среднее для всех пород видовое число f = 0,472. Угол визирования в приборе В.М. Иванюты переменный и зависит от средней высоты древостоя, которая определяется предварительно. Запас древостоя (м3/га) составляет: М =10n, где n – число учетных деревьев. Норвежский ученый Л. Странд разработал метод определения запаса древостоя с помощью угловых проб и перечета деревьев. Странд в основу метода положил угловые пробы, закладываемые в вертикальной плоскости. Форма проб у Странда получается прямоугольная. Длина одной стороны прямоугольника принимается постоянной, равной Другая сторона является переменной, изменяющейся пропорционально средним высоте и диаметру древостоя. Длина переменной стороны находится по шкале тангенсов, имеющейся в реласкопе Биттерлиха. Странд предлагает, длину пройденного пути по визиру принять постоянной При этом визируют на основание и вершину дерева. Если эти две точки визирования лежат по разные стороны горизонтали, то результаты отсчетов суммируются. В противном случае из результата визирования на вершину вычитается отсчет, полученный при визировании на основание дерева.
а б Рисунок 11.6 Схема пробной площади Странда а – вид по вертикали; б – вид по горизонтали
Если полученный результат превышает число 50, то это означает, что дерево подлежит учету, так как оно находится в пределах пробы, имеющей длину стороны, равную половине высоты древостоя (рисунок 11.6-- а). Площадь прямоугольной пробы при указанной длине ее сторон будет следующей:
а в долях гектара
А - площадь пробы; h — средняя высота древостоя. Площадь поперечного сечения одного дерева:
Объем цилиндра, имеющего со средним деревом равные основания (g) и высоту (h):
Разделим объем цилиндра на площадь пробы:
Соответственный расчет дает сумму площадей сечения древостоя, м2/га:
Отсюда запас древостоя равен М= GHF, Предложение Странда представляет интерес в том отношении, что оно открывает новые возможности применения угловых проб. Взяв за основу идею В. Биттерлиха и поставив несложную, но остроумно решенную математическую задачу, Странд вывел весьма простые формулы, определяющие запас и сумму площадей поперечных сечений деревьев на 1га. Этим он пополнил теорию и технику определения запасов и сумм площадей сечений древостоев. Пробные площади, закладываемые по методу Странда, имеют весьма ограниченные размеры. Между тем величине древесного запаса в пределах одного и того же таксационного участка свойственно большое варьирование. Вследствие этого пробные площадки незначительных размеров не гарантируют нахождения запасов с достаточной точностью. Отмеченный недостаток можно устранить путем закладки большого числа проб, равномерно размещенных по таксируемому участку. Однако в этом случае возрастают затраты труда на отграничение проб в натуре и раздельную таксацию леса на каждой из этих проб. Лучшим решением поставленной задачи следует считать увеличение в 5 или 10 раз размера (15,7 м) постоянной стороны прямоугольной пробы. В этом случае формулы Странда, определяющие запас и суммы площадей поперечных сечений деревьев на 1га, будут следующими:
Соответственно этим формулам при таксации леса по методу Странда в лесу надо закладывать прямоугольные пробы, имеющие ширину, пропорциональную высоте и диаметрам деревьев таксируемого древостоя. Длина пробных площадей должна соответствовать коэффициентам формул 78,5 или 157м. При таком решении задачи мы закладываем фактически ленточную пробную площадь, пересекающую значительную часть таксируемого древостоя и, таким образом, аккумулирующую в себе все его особенности. Пробные площадки должны отражать характерные особенности всей площади насаждения. Деревья, имеющиеся на пробных площадках, измеряются, и на основе этих измерений вычисляется запас. Выше было показано, что ленточные пробы при неравномерном размещении деревьев, что является обычным в лесу, часто приводят к систематическим ошибкам. Результаты обмеров деревьев на пробных площадках в конечном итоге должны давать полную картину, характеризующую все насаждение. Поскольку метод Странда не гарантирует отсутствия систематических ошибок, особенно в смешанных древостоях и в насаждениях, пройденных рубками ухода, то широкого распространения у нас он не получил.
|

 =71100 см2. Если на окружности описанного круга окажется три дерева диаметром 2см каждое, то площадь их поперечного сечения будет равна З
=71100 см2. Если на окружности описанного круга окажется три дерева диаметром 2см каждое, то площадь их поперечного сечения будет равна З  1см2.
1см2.

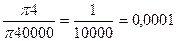 .
.
 и числом квадратных метров в 1га - с другой, и надо воспользоваться для перехода от числа деревьев к сумме площадей сечений деревьев на 1га. При таком решении вопроса сумма площадей сечения деревьев каждой ступени толщины определяется в долях площади пробы. В обоих случаях доли площади имеют общий знаменатель (10 000). При наличии общего знаменателя для нахождения суммы дробных величин необходимо лишь суммировать числители. Полученный результат показывает в десятитысячных долях единицы сумму площадей поперечных сечений деревьев всех ступеней толщины, имеющихся на круговых пробах.
и числом квадратных метров в 1га - с другой, и надо воспользоваться для перехода от числа деревьев к сумме площадей сечений деревьев на 1га. При таком решении вопроса сумма площадей сечения деревьев каждой ступени толщины определяется в долях площади пробы. В обоих случаях доли площади имеют общий знаменатель (10 000). При наличии общего знаменателя для нахождения суммы дробных величин необходимо лишь суммировать числители. Полученный результат показывает в десятитысячных долях единицы сумму площадей поперечных сечений деревьев всех ступеней толщины, имеющихся на круговых пробах.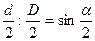 (11.2)
(11.2)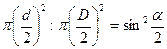 (11.3).
(11.3).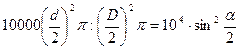 (11.4).
(11.4).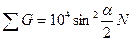 (11.5.)
(11.5.) представляет собой числовой множитель. Угол визирования у прибора надо выбирать такой, при котором этот множитель был бы равен целому числу. Более удобен для пользования прибор, для которого множитель
представляет собой числовой множитель. Угол визирования у прибора надо выбирать такой, при котором этот множитель был бы равен целому числу. Более удобен для пользования прибор, для которого множитель  (м2) на 1га насаждения.
(м2) на 1га насаждения.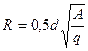 , (11.6)
, (11.6)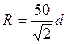
 ;; R = 35,355 м;
;; R = 35,355 м; , ( 11.7 ),
, ( 11.7 ),
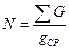 ,где
,где
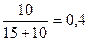
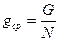 . Отсюда средний диаметр древостоя:
. Отсюда средний диаметр древостоя:  . В приведенной таблице (11.5) в первой графе даны диаметры на высоте груди в сантиметрах, во второй графе – площадь сечения в метрах квадратных, соответствующая этим диаметрам. В третьей графе приведено число учтенных деревьев
. В приведенной таблице (11.5) в первой графе даны диаметры на высоте груди в сантиметрах, во второй графе – площадь сечения в метрах квадратных, соответствующая этим диаметрам. В третьей графе приведено число учтенных деревьев
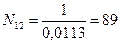
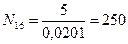
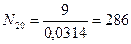



 ), примерно 4%. Такая точность (около 5%) вполне удовлетворяет лесоустроительную практику.
), примерно 4%. Такая точность (около 5%) вполне удовлетворяет лесоустроительную практику.
 ,где n- число учетных деревьев. деревьев категории i,закрывающих просвет прицела. Высоту дерева hi уподобим радиусу и им опишем круг. Его площадь будет равна πh2i, м2, а сумма площадей кругов, описываемых радиусом hi составит ti tg2β м2.
,где n- число учетных деревьев. деревьев категории i,закрывающих просвет прицела. Высоту дерева hi уподобим радиусу и им опишем круг. Его площадь будет равна πh2i, м2, а сумма площадей кругов, описываемых радиусом hi составит ti tg2β м2.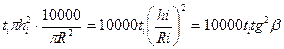 м2.
м2. , a площадь всех кругов равна 10 000 t tg2 βм2.
, a площадь всех кругов равна 10 000 t tg2 βм2. ,
, . (11.7).
. (11.7). . Отсюда средняя высота равна
. Отсюда средняя высота равна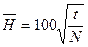 . (11.8).
. (11.8). , (11.9), где
, (11.9), где м.
м.
 ,
,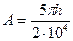 , где
, где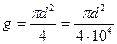 м2.
м2.

 ,
, (11.10)
(11.10) при L = 15,7 .5 = 78,5 м;
при L = 15,7 .5 = 78,5 м; при L = 15,7 . 5 = 78,5 м;
при L = 15,7 . 5 = 78,5 м; при L = 15,7 · 10 = 157 м;
при L = 15,7 · 10 = 157 м;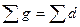 при L = 15,7 · 10 = 157 м.
при L = 15,7 · 10 = 157 м.


