Определение прироста у растущих деревьев
Если при определении прироста на срубленном стволе мы встречаемся только с техническими трудностями, то при вычислении прироста растущего дерева нас ожидают методические проблемы. На растущем дереве мы лишены возможности измерить прирост по радиусу на отрезках по высоте дерева. Известную неопределенность вносит и невозможность точного установления прироста по высоте, особенно у деревьев, не образующих мутовки. Поэтому основным измеряемым показателем остается прирост по радиусу или диаметру на доступной нам высоте – 1,3 м. В принципе современные приборы могут обеспечить измерение диаметра и прироста на любой высоте. Но такие приборы дороги, работа с ними идёт очень медленно. Поэтому измерение прироста растущего дерева столь трудоемким способом экономически нецелесообразно. Названный метод может применяться в исключительных случаях В обычной практике исследований прирост дерева находят через процент прироста. За основу здесь берется вышеприведенная формула Пресслера (14.45).
Объем дерева принимаем равным: в данное время Va = ghf; а n лет назад Va-n = g1 h1 fi. Подставляем эти обозначения в формулу (14.45), получим
Если допустить, что за n лет высота и видовое число остались неизменными, формула, определяющая процент прироста по объему, примет следующий вид:
отсюда
Для упрощения вычислений введем в формулу относительный диаметр.Относительным диаметром r называется частное от деления диаметра без коры d в данный момент на его прирост Zd за n лет: r = d / Z d, отсюдаd = rZd.. Диаметр d1, который имело дерево год назад, обозначим через d-Zd.. В этом случае можно написать d1 = d -Zd = rZd - Zd (r-1). (14.52) Подставив эти величины в формулу для нахождения процента прироста по объему, выраженного формулой Пресслера, т. е.
получим
Формула (13.23), определяющая процент прироста по объему в зависимости от величины относительного диаметра, применима для деревьев, у которых прирост в высоту прекратился. Для деревьев, имеющих прирост в высоту, показатели степени в формуле должны соответственно измениться. По мере увеличения роста в высоту показатель степени также увеличивается. По опытным данным, величина его колеблется от 2 до 4. Исходя из этого, формуле Пресслера, определяющей процент прироста по относительному диаметру, можно придать следующий общий вид:
Исследования показали, что у большей части стволов показатель степени изменяется от 2 до 3,5. Процент прироста по объему для деревьев, у которых прирост в высоту прекратился и форма ствола осталась неизменной, определяется по формуле pv = pg = 2 pd = 200 Zd / d Годичный прирост по диаметру Zd равен удвоенному приросту по радиусу 2Zr. Отсюда получим pv = 200 . 2Zr / d = 400 Zr / d. Годичный прирост по радиусу Zr представляет не что иное, как ширину одного годичного слоя. Обозначим ее через i. Тогда формула примет такой вид: pv = 400 i / d. (14.55)
При определении ширины годичного слоя подсчитывают число слоев n на последнем сантиметре толщины ствола. Разделив 1 см на число слоев n, получим среднюю ширину годичного слоя 1 / n. Подставив в формулу (14.55) вместо i величину i / n, получим следующую формулу, определяющую процент текущего прироста: pv = 400 / dn. Эта формула еще в прошлом столетии была предложена немецким лесоводом Шнейдером. Для деревьев, имеющих прирост по высоте, соответственно интенсивности этого прироста коэффициент, стоящий в числителе формулы, увеличивается. Коэффициент 400 соответствует показателю степени x в формуле (14.54), равному 2. Отсюда на единицу показателя степени приходится коэффициент 400 / 2 = 200. При определении по выведенной формуле процента прироста для данного дерева надо на этот показатель умножить коэффициент 200. Если диаметр дерева без коры принять 38 см, а число слоев на 1 см радиуса равным 10, процент прироста по объему составит
Коэффициент, стоящий в числителе формулы, изменяется в зависимости от длины кроны и интенсивности роста в высоту. Поэтому рассмотренной формуле следует придать такой общий вид: pV = Ki / d, или pV = K / dn. При определении прироста необходимо учитывать соотношение между приростом по высоте и по диаметру. Связь этих двух величин проф. Г.М. Турский характеризует таким уравнением: ha-n / ha = (da-n / da)k. (14.56) Показатель степени k характеризует особенности роста деревьев. Если k принять равным единице, формула примет следующий вид: ha-n / ha = da-n / da. (14.57) В этом случае рост дерева в высоту пропорционален росту в толщину. Такой рост называют нормальным. При нормальном росте видовое число остается неизменным и ствол во всех своих частях сохраняет в росте пропорциональность. При k=0 отношение ha-n / ha = 1. Такой характер роста наблюдается у деревьев, прекративших прирост в высоту, т. е. это старые деревья с отмирающей верхушкой. Анализируя различные соотношения прироста по высоте и диаметру, можно прийти к выводу, что чем больше k, тем энергичнее рост в высоту в сравнении с ростом в толщину. На основании уравнения (14.56) находим, что
Нам известно, что процент прироста по объему можно найти по формуле (14.19)
Эту формулу выразим следующим образом:
Допустим, что в течение n лет видовое число ствола остается неизменным. Тогда этой формуле можно придать такой вид:
Подставив x вместо k+2, получим
При замене абсолютных диаметров относительными выше была получена формула (14.61):
Мы уже говорили, что у большей части стволов показатель степени изменяется от 2 до 3 1/3. Разделив разность между этими числами на пять частей, получаем следующие нормативы для показателя степени: 2; 2,4; 2,7; 3 и 3,3. Основываясь на правилах сложных процентов и разложив полученные величины в ряды по биному Ньютона, в результате математических преобразований Г.М. Турский получил следующую формулу для определения процента прироста по объему: pV = K pd,(14.62)
или
Ранее, когда расчеты велись лишь вручную, для упрощения счета составлялись вспомогательные таблицы и номограммы. Н.П. Анучин разработал номограмму, где по величине диаметра дерева и радиального прироста на 1.3 м определяются процент прироста и его абсолютная величина. Так как вычисления прироста обычно делают в лабораторных условиях, где есть компьютеры, то вспомогательные таблицы и номограммы практически потеряли своё значение. В силу того, что при нахождении процента прироста растущего дерева используется относительно субъективный показатель (энергия роста в высоту) и при этом пользуются формулами для определения объема, описанный метод имеет невысокую точность: 15-30%. Прирост отдельного растущего дерева в практике вычисляется очень редко. В практике работы лесхозов обычно не применяются. Гораздо больше значение имеет определение прироста древостоя.
|

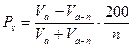 (14.45)
(14.45)
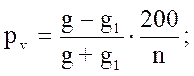 g = p d2 / 4, g1 = p d12 / 4,
g = p d2 / 4, g1 = p d12 / 4,
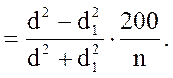
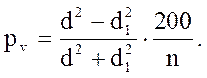
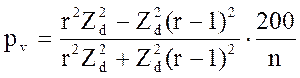
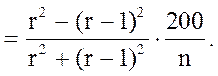 (14.53)
(14.53)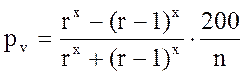 (14.54)
(14.54)
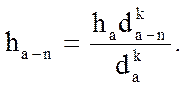 (14.58)
(14.58)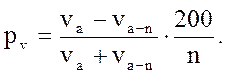
 (14.59)
(14.59)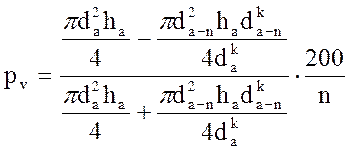

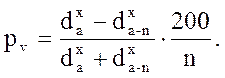 (14.60)
(14.60) (14.63)
(14.63)


