5B071200– Машиностроение», 5B09 0100 - «Транспорт, транспортная техника и технологии»
Ответственный за разработку тестов – к.т.н., и.о. доцента Омарова Н.И.
| №
| Уровень сложности
| Вопрос
| Раздел, тема
| Ответ А
| Ответ В
| Ответ С
| Ответ Д
| Ответ Е
|
|
|
| Какие тела абсолютно свободные?
| 1.1
| Которые могут совершать любые перемещения в пространстве.
| Которые вращаются
| Которые не деформируются
| Перемещения которых в каких-либо направлениях ограничены
| Которые могут перемещаться по горизонтали
|
|
|
| В каком случае две силы находятся в равновесии?
| 1.2
| Если они равны по модулю и действуют по одной линии действия в противоположные стороны
| Если они будут равны по модулю
| Если они противоположны по направлению
| Если они направлены по одной линии действия
| Если они действуют по одной линии действия в противоположные стороны
|
|
|
| Какие характерные точки имеет сила на чертеже?
| 1.2
| Начало и конец силы
| Начало силы
| Модуль силы
| Направление силы
| Линию дейс-твия силы
|
|
|
| Какие системы сил являются эквивалентными?
| 1.2
| При замене одной системой сил другой системой – состояние тела не изменяется
| Равные по модулю
| Уравновешенные
| Противоположные по направлению
| Направленные под углом 450 друг к другу
|
|
|
| Что значит сила – равнодействующая?
| 1.2
| Сила – эквивалентная системе сил
| Сила инерции
| Центробежная сила
| Уравновешивающая сила
| Реактивная сила
|
|
|
| Чему равна уравновешивающая сила?
| 1.2
| Равная по модулю равнодействующей но направлена в противоположную сторону по линии действия
| Сумме всех сил, действующих на тело
| Разности сил, действующих на тело
| Равна равнодействующей и направлена в ту же сторону
| Диагонали параллелограмма построенного на этих силах
|
|
|
| Измениться ли состояние тела если к нему добавить или отнять уравновешенную систему сил?
| 1.2
| Согласно 3 аксиоме статики – нет
| Согласно закону динамики – измениться
| Тело будет двигаться уравновешивающую
| Тело будет вращаться
| Тело будет перемещаться равно-ускоренно
|
|
|
| Как определить равнодействующую двух сил, направленных под углом к друг другу?
| 1.2
| Изображается диагональю параллелограмма, построенного на этих силах
| Нужно построить силовой треугольник из этих сил
| Нужно построить прямоугольник из этих сил
| Силовой треугольник должен быть замкнут
| Параллелограмм разомкнут
|
|
|
| В чем сущность принципа отвердения?
| 1.2
| Равновесие сохраняется и после того как система отвердеет или станет абсолютно твёрдой
| Равновесие нарушается если система отвердеет
| Равновесие на нарушается если тело остановится
| Равновесие нарушается если только остановиться
| Вращение тела прекратиться
|
|
|
| Как определить графически равнодействующую пучка сил на плоскости?
| 1.3
| Нужно построить силовой ногоугольник из этих сил
| Построить параллелограмм
| Построить силовой треугольник
| Построить силовой четырёх угольник
| Построить ромб
|
|
|
| В чём заключается графическое условие равновесия пучка сил на плоскости?
| 1.3
| Силовой многоугольник построенный из этих сил -замкнут
| Силовой треугольник не замкнут
| Равнодействующая равна нулю
| Силовой многоугольник разомкнут
| 1.∑xi = 0
2.∑yi = 0
|
|
|
| В чём заключается аналитические условия равновесия пучка сил на плоскости?
| 1.3
| 1.∑xi = 0
2. ∑yi = 0
| R = 0
| 1. ∑Mx = 0
| 1.∑MA = 0
2.∑MB = 0
| 1.∑MA = 0
2.∑Mi = 0
|
|
|
| Чему равна проекция равнодействующей силы пучка сил на оси координат?
| 1.3
| Rx = ∑xi
Ry = ∑yi
| Rx = Ry = ∑xi
| Rx = Ry = ∑yi
| Rx = Rcos α
| Ry = Rsin α
|
|
|
| Чему равна равнодействующая сила R пучка сил, находящегося в равновесии?
| 1.3
| R = 0
| R = √Rx2 + Ry2
| R = √(∑xi)2 + (∑yi)2
| R = Rα + Ry
| R = Rysinα
|
|
|
| На каком из рисунков правильно построен силовой четырёхугольник трёх сил?

| 1.4
|
   b F2 с
F3 b F2 с
F3
  F1 R d
a
F1 R d
a
|   b
b  
  F1 F2 с F1 F2 с
 R F3
d R F3
d
|
c
 
  F2 F3 F2 F3
 b
R d
F1
a b
R d
F1
a 
|  b
F1 b
F1
   a F3 c a F3 c
 R
F2
d
R
F2
d
|
a F2 b

 R F1
c R F1
c
|
|
|
| Какие силы параллельны?
| 1.4
| Направленные в одну сторону, линии действия которых параллельны между собой
| Равные по модулю
| Противоположные по направлению
| Которые на пересекаются
| Которые лежат в одной плоскости
|
|
|
| Какие силы антипараллельные?
| 1.4
| Направленые в противоположные стороны, линии действия которых параллельны
| Равные по модулю
| Противоположные по направлению
| Которые лежат в одной плоскости
| Которые не пересекаются
|
|
|
| Что такое пара сил?
| 1.4
| Две равные по модулю антипараллельные силы, приложенные к твёрдому телу
| Две равные по модулю параллельные силы
| Две антипараллельные силы
| Которые не имеют равнодействующей
| Которые не равны по модулю
|
|
|
| Какие две пары будут статистически эквивалентные.
| 1.4
| У которых моменты равные
| У которых моменты разные
| Момент одной пары в два ра-за больше момента второй пары
| У которых плечи равные
| У которых силы равные по модулю
|
|
|
| Определить проекции силы на оси
х и у

| 1.4
| X = Fcosα
Y = Fsinα
| X = Y= sinα
| Y = tgα
| X = ctgα
| X + Y = F
|
|
|
| В каком случае пары сил находятся в равновесии?
| 1.4
| Если алгебраическая сумма моментов равна нулю
| Если
1.∑xi = 0
2. ∑yi = 0
| Если
МА = 0
| Если
M = Fh
| Если сила параллельна оси
|
|
|
| Чему равен момент равнодейс-твующей паре?
М1=40кН М2=20кН
М3=20кН

| 1.4
| MR = M1 – M2 – M3 = 40 – 20 – 20 = 0
Пары сил находятся в равновесии
| MR = M1 = 40 кН
| MR = M1 – M2 = 40 – 20 = 20 кН
| MR = M1 - M3 = 40 – 20 = 20 кН
| MR = 2M1 = 2 *40 = 80кН
|
|
|
| Чему равен момент силы, относительно точки, показанной на рисунке

| 1.4
| Нулю, так как плечо силы равно нулю
| 2F
| F
| 3F
| M0 = 2Fl
|
|
|
| Можно ли силу перенести параллельно самой себе в любую точку твёрдого тела?
| 1.4
| Можно, но при этом добавится пара сил
| Нельзя, нарушится равновесие
| Можно, не нарушая равновесия
| Нельзя, при этом тело начнёт пере-мещаться
| Можно, но при этом добавиться две пары сил
|
|
|
| Что необходимо для того чтобы пространственная система сходящихся сил находилась в равновесии?
| 1.4
| Чтобы
- ∑xi = 0
- ∑yi = 0
- ∑zi = 0
| Чтобы
1. ∑xi = 0
2. ∑yi = 0
| Чтобы
- ∑xi = 0
- ∑zi = 0
| Чтобы
- ∑zi = 0
| Чтобы
1. ∑zi = 0
2. ∑yi = 0
|
|
|
| Укажите какой вид имеет 1ая форма аналитических условий равновесия плоской системы произвольно расположенных сил?
| 1.4
| - ∑xi = 0
- ∑yi = 0
- ∑МА = 0
| 1. ∑xi = 0
2. ∑МА = 0
| - ∑yi = 0
- ∑МВ=0
| 1. ∑МА = 0
2.∑МВ=0
| 1. ∑yi = 0
2. ∑МС=0
|
|
|
| Укажите какой вид имеет 2ая форма аналитических условий равновесия плоской системы произвольно расположенных сил?
| 1.4
| 1. ∑МА = 0
2.∑МВ=0
3. ∑xi = 0
| 1. ∑МА = 0
2. ∑xi = 0
| 1. ∑МА = 0
2.∑МВ=0
3.∑МС=0
| 1.∑МВ=0
2.∑xi = 0
3.∑yi = 0
| 1.∑МА = 0
2.∑yi = 0
3.∑МВ=0
|
|
|
| Укажите какой вид имеет 3 форма аналитических условий равновесия плоской системы произвольно расположенных сил?
| 1.4
| 1. ∑МА = 0
2.∑МВ=0
3.∑МС=0
| 1.∑МА=0
2.∑xi = 0
3.∑yi = 0
| 1. ∑МА = 0
2.∑МВ=0
3. ∑xi = 0
| 1.∑МВ=0
2.∑МС=0
3.∑yi = 0
| 1. ∑МА = 0
2. ∑xi = 0
3.∑МС=0
|
|
|
| Что необходимо чтобы пучок сил находился в равновесии?
| 1.4
| Силовой многоуголь-ник построенный из этих сил должен быть замкнут
| Необходимо чтобы
R = 10F
| Необходимо чтобы
R = 2F
| Необходимо чтобы
R = 4F
| Необходимо чтобы
R = -2F
|
|
|
| Сколько аналитических условий равновесия имеет пространственная система произвольно расположенных сил?
| 1.5
| 1. ∑xi = 0
2.∑yi = 0
3.∑zi = 0
4. ∑МX = 0
5. ∑МY=0
6.∑МZ=0
| 1. ∑xi = 0
2.∑МZ=0
3. ∑МY=0
| 1.∑yi = 0
2.∑МZ=0
3. ∑МX = 0
| 1.∑МZ=0
2. ∑МX = 0
3. ∑МY=0
| 1. ∑МX = 0
2. ∑МY=0
3.∑МZ=0
|
|
|
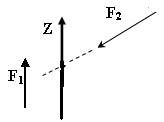
| Чему равны моменты изображённых на рисунке сил, относительно оси Z?
| 1.5
| Нулю, т.к. одна из сил F1, параллельна оси, а вторая F2 её пере-секает в пространстве
| МZ=2F1
| МZ=2F2
| МZ=F1 + F2
| MZ = -(F1/F2)
|
|
|
| Какие аналитические условия равновесия пространственой системы параллельных оси Z сил применимы при решении задач?
| 1.5
| 1.∑Zi=0
2. ∑МX = 0
3. ∑МY=0
| 1. ∑xi = 0
2.∑yi = 0
3.∑МX = 0
| 1. ∑xi = 0
2. ∑МX = 0
3. ∑МY=0
| 1. ∑МX = 0
2. ∑МY=0
3.∑МZ=0
| 1. ∑МX = 0
2.∑МZ=0
3. ∑xi = 0
|
|
|
| Если силы параллельны оси X в пространстве, то какие условия равновесия применимы?

| 1.5
| 1. ∑XI = 0
2. ∑МY=0
3.∑МZ=0
| 1. ∑xi = 0
2.∑yi = 0
3.∑МX = 0
| 1. ∑xi = 0
2.∑zi = 0
3.∑МY = 0
| 1. ∑xi = 0
2. ∑МX = 0
3.∑МZ=0
| 1. ∑xi = 0
2. ∑МX = 0
3. ∑МZ=0
|
|
|
| Если силы параллельны оси Y в пространстве, то какие условия равновесия применимы?
| 1.5
| 1. ∑yi = 0
2. ∑МX = 0
3.∑МZ=0
| 1. ∑xi = 0
2.∑zi = 0
3.∑yi = 0
| 1. ∑yi = 0
2. ∑МY = 0
3.∑МZ=0
| 1. ∑МX = 0
2.∑МZ=0
3. ∑МY=0
| 1.∑МY = 0
2. ∑xi = 0
3. ∑yi = 0
|
|
|
| Составить уравнение проекций заданных сил на ось Z

| 1.6
| ∑Zi =0
-F-N3cos450=0
| ∑Zi =0
-F-N3sin650=0
| ∑Zi =0
-2N1-N3cos450=0
| ∑Zi =0
N1-N2- N3=0
| ∑Zi =0
F-N3- N2=0
|
|
|
| Составить уравнение моментов относительно точки с левой части рамы

| 1.3
| ∑МСЛЕВ= - HA*6 + υA*2 – F*3 – g*2*1=0
| МС=υA*2
| МС=υA*2
| МС=g*2*1+HA*3
| МС=–F*3 +
HA*6
|
|
|
| Определить уравнение проекций заданных сил на ось Y

| 1.3
| ∑Yi=-N3sin450-N1sin600-N2sin600
| ∑Yi=0
| ∑Yi=-F
| ∑Yi= -2N2sin600
| ∑Yi=-2F-N3
|
|
|
| Определить уравнение проекций заданных сил на ось X 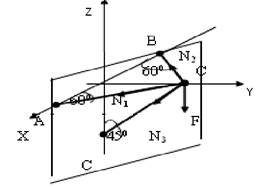
| 1.3
| ∑Хi=
N1cos600-
N2cos600
| ∑Хi=0
| ∑Хi=-F
| ∑Хi=-N3cos600-2F
| ∑ХC= -2N2cos600-N3
|
|
|
| Определить проекции заданных сил на ось Z 
| 1.3
| ∑ZI=-F-N3*cos450
| ∑ZI=0
| ∑ZI=-2F
| ∑ZI=
-N3*cos600
| ∑ZI=-F-2N3
|
|
|
| Что такое центр параллельных сил?
| 1.3
| Точка через которую проходит линия действия равнодей-ствующей этой системы
| Центр тяжести
| Центр окружности
| Центр шара
| Центр масс
|
|
|
| По каким формулам определяется координаты центра параллельных сил на плоскости?
| 1.3
|  
| 
| XC=2R
YC= 0
| XC=0.424R
YC=0
| 

|
|
|
| Что такое центр тяжести тела?
| 1.3
| Точка, неизменно связанная с телом, через которую проходит линия действия веса тела
| Центр окружности
| Центр шара
| Центр масс
| Центр параллельных сил
|
|
|
| Если сечение имеет две или более осей симметрии, о где находиться её центр тяжести?
| 1.4
| На пересечении этих осей
| В центре
| На расстояние 
| XC=0.424R
| YC=2R/2
|
|
|
| Правильно ли указано на рисунке положение центра тяжести прямоугольного треугольника?

| 1.4
| Находиться на пересечении двух прямых параллельных катетам, как указанно на рисунке
| Нет
| XC=1/4b
YC=1/4h
| XC=0,42h
YC=0,2b
| XC=YC=h/2
|
|
|
| Чему равно расстояние YC у полукруга
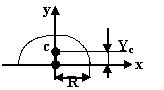
| 1.4
| YC=0,424R
| YC=2R
| YC=D/2
| YC=R
| YC=R/2
|
|
|
| Чему равна площадь параболического треугольника?

| 1.4
| А=2/3bh
| А=1/2bh
| А=1/3bh
| A=bh
| A=2bh
|
|
|
| Чему равна площадь параболического треугольника, указанного на рисунке?
 
| 1.4
| А=1/3bh
| А=1/2bh
| А=2/3bh
| A=bh
| A=2bh
|
|
|
| Правильно ли показанно положение центра тяжести фигуры на чертеже?

| 1.4
| Да
XC=3/8b
YC=3/8h
| Нет
XC=1/2b
YC=h
| Нет
XC=h/2
YC=b
| Нет
XC=h/2
YC=b/2
| Нет
XC=h
YC=b
|
|
|
| Как определить площадь полукруга радиуса R?
| 1.4
| А=Пd2/8
| А=Пd2/4
| А=Пd2/12
| А=2Пd2
| А=4/3ПR2
|
|
|
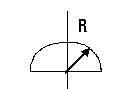
| Где находиться центр тяжести у полукруга?
| 1.4
| На оси симметрии, на расстоянии YC=0,424R от горизонтального диаметра
| YC=2R
| YC=XC=R/2
| YC=XC=D/2
| XC=R
YC=2R
|
|
|
| Укажите по каким формулам определяются координаты центра тяжести плоской фигуры?
| 1.4
|  
|  
| 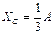 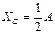
|  
| 
|
|
|
| Укажите правильно составленные уравнения для нахождения координат центра тяжести изображённой на чертеже фигуры.

| 1.4
|  
|  
|  
|  
|  
|
|
|
| Укажите правильно составленные уравнения координат центра тяжести изображённой на чертеже фигуры

| 1.4
|  
|  
|  
| 
|  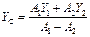
|
|
|
| Где находится центр тяжести у двутавра?

| 1.4
| На пересечении осей симметрии
| В середине полки
| На вертикальной стенке
| На верхней полке
| На нижней полке
|
|
|
| Где находится центр тяжести у равнополочного уголка?

| 1.4
| На расстояниях ХС=УС от горизонтальной и вертикальной полок
| На расстоянии Z0 от вертикальной полки
| На расстоянии Х0 от стенки
| На оси симметрии
| На бесконечно малом расстоянии от горизонтальной полки
|
|
|
| Где находится центр тяжести у неравнополочного уголка?

| 1.4
| На расстояниях ХС и УС от вертикальной и горизонтальной полок
| На расстоянии Z0 от вертикальной полки
| На расстояниях
Х0=У0 от полок
| На расстоянии ХС=b/2
Y0=b/2
| На расстоянии ХС=b/2
Y0=b/3
|
|
|
| Какое равновесие твёрдого тела имеющего точку подвеса, изображённого на рисунке?

| 1.5
| Устойчивое, которое восстанавливается после удаления внешних сил силами самой системы
| Не устойчивое
| Безразличное
| Уравновешенное
| Постоянное
|
|
|
| Каким равновесием обозначается тело, изображённое на рисунке?

| 1.5
| Устойчивым
| Не устойчивым
| Безразличным
| Постоянным
| Уравновешенным
|
|
|
| Каким равновесием обладает тело, изображённое на рисунке

| 1.5
| Не устойчивым
| Устойчивым
| Постоянным
| Безразличным
| Уравновешенным
|
|
|
| Каким равновесием обладает тело, изображённое на рисунке

| 1.5
| Безразличным
| Не устойчивым
| Устойчивым
| Уравновешенным
| Постоянное
|
|
|
| Чему равен опрокидывающий
момент?

| 1.5
| Moн=Fh
| Moн=G(a/2)
| Moн=F(a/2)
| Moн=Gh
| Moн=(F+G)a/2
|
|
|
| Чему равен удерживающий момент?

| 1.5
| MY=G(a/2)
| MY=Fh
| MY=Gh
| MY=F(a/2)
| MY=(F+G)a/2
|
|
|
| Как определяется коэффициент запаса устойчивости?
| 1.5
| KY=MY/Mно
| KY= Mно /MY
| KY= 2Mно
| KY=2MY
| KY=2MY/Mно
|
|
|
| Какие деформации остаточные?
| 1.3
| Которые не исчезают после снятия нагрузки
| Вогнутые
| Выпуклые
| Кручения
| Изгиба
|
|
|
| До каких пор тело будет сохранять состояние покоя?
| 1.3
| Пока другие силы или тела не выведут его из этого состояния
| Постоянно
| Временно
| Пока сохраняется равновесие
| Пока не изменит направление
|
|
|
| Укажите по какой формуле определяется момент силы относительно точки
| 1.2
| MC=±Fh
| MC=F+h
| MC=Fl3
| MC=2Fb
| MC=F1+F2
|
|
|
| Что такое центр параллельных сил?
| 1.3
| Точка через которую проходит линия равнодействующей системе параллельных сил
| Точка равновесия тела
| Точка вращения тела
| Точка устойчивости тела
| Точка опрокидывания тела
|
|
|
| В каком состоянии находяться две равные по модулю силы, изображённые на рисунке?

| 1.2
| В равновесии
| В движении
| В вращательном движении
| В состоянии несовместимости
| В переносном движении
|
|
|
| Если деформации тела полностью исчезают после снятия нагрузки, то как они называются?
| 1.2
| Упругие
| Остаточные
| Изгиба
| Кручение
| Не восстанавливающиеся.
|
|
|
| Если сила заменяет действие целой системы сил, то как она называется?
| 1.2
| Равнодействующая сила
| Уравновешивающая сила
| Вращательная сила
| Центробежная сила
| Сила инерции
|
|
|
| Связь гибкая нить, может ли реакция связи направлена так, как показанно на рисунке?

| 1.2
| Нет, реакция может быть направлена только от тела к связи по связи
| Может, если нить отвердеет
| Не, реакция связи должна действовать вне связи
| Силы равны по модулю
| Противоположны по направлению
|
|
|
| Изменяется ли состояние тела, если силу, показанную на рисунке перенести в точку В?
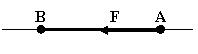
| 1.2
| Нет, на основании следствия из 2 и 3 аксиом статики
| Тело начнёт вращаться
| Сила- вектор скользящий
| Сила величина скалярная
| Силу можно заменить системой сил.
|
|
|
| Если сила эквивалентна равнодействующей системе сил, на направление в противоположную сторону по линии действия, то как она называется?
| 1.2
| Уравновешивающей силой
| Противодействующей силой
| Главным вектором
| Главным моментом
| Вектором момента пары сил
|
|
|
| Если линии действия всех сил, действующих на твёрдое тело пересекаются в одной точке, то как называется такая система сил?
| 1.2
| Система сходящихся сил или пучок сил
| Система параллельных сил
| Система произвольно расположенных сил
| Система пространственных сил
| Система сил, лежащих в одной плоскости
|
|
|
| Какая система сил изображаена на рисунке?

| 1.3
| Пара сил. Две равные по модулю антипараллельные силы
| Две параллельные силы
| Две антипараллельные силы
| Плоская система сил
| Плоская система параллельных сил
|
|
|
| Как называется тела, препятствующие перемещению абсолютного свободных тел, превращая их в несвободные?
| 1.2
| Называются связями
| Ограничители
| Препятствиями
| Упорами
| Выступами
|
|
|
| Сколько реакций связей возникает в изображённом виде связи?

|
| Две, вертикальная υа и горизонтальная На
| Одна, вертикальная υа
| Одна горизонтальная НА
| Одна реактивный момент
| Две, вертикальные υА и реактивный момент МА
|
|
|
| Сколько реакций связей возникает в изображённом виде связи?

| 1.2
| Три – вертикальная υА, горизонтальная НА и реактивный момент в защемлении МА
| Одна – реактивный момент в защемлении МА
| Две – вертикальная υА и горизонтальная НА
| Две, вертикальная
υА и реактивный момент в защемлении МА
| Одна вертикальная υА
|
|
|
| Если силовой многоугольник построенный из пучка сил замкнуть то в каком состоянии будет находиться система сил?
| 1.2
| Равнодействующая система сил равна нулю, система сил находиться в равновесии
| Уровновешивающая сила равна нулю
| Равнодействующая сила отрицательна
| Тело движется равномерно
| Тело вращается
|
|
|
| Пары сил, моменты которых равны как называются
| 1.3
| Статический эквивалентны
| Уровновешенные
| Одинаковые
| Вращающие тело по часовой стрелке
| Вращающие тело против часовой стрелки
|
|
|
| Чему равен момент заданной пары сил

| 1.2
| M=F1*2=4*2
=8кНм
| M=2F1=2*4
=8кН
| M=2F1*2=
2*4*2=16кН
| M=-F2*2=4*2
=8кН
| M=2F2*F1=
2*4*4=32кН2
|
|
|
| В каком состоянии находиться система пар сил, указанных на рисунке?
Чему равен момент равнодействующей паре?
М1=20кН М2=20кН М3=40кН

| 1.3
| В равновесии т.к МR=-М1-М2+М3= -20-20+40=0
| Вращается по часовой стрелке
| Вращается против часовой стрелки
| Движутся поступательно
| Находится в неопределённом состоянии
|
|
|
| Тела, препятствующие перемещению абсолютно свободных тел, преврая их в несвободные, называются

| 1.2
| Связями. Горизонтальная опорная поверхность
| Стержнями
| Гибкой нитью
| Шарнирно подвижной опорой
| Жёсткий защемлением
|
|
|
| Сколько реакций возникает в указанном на рисунке виде связи?
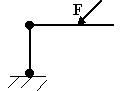
| 1.2
| Одна,перпендикулярна к опорной по-сти и проходящая через центр верхнего, шарнира
| Две –вертикальная и горизонтальная
| Две – вертикальная и реактивным момент
| Две горизонтальная и реактивным момент
| Три вертикальная, горизонтальная и реактивным момент
|
|
|
| Если тело сохраняет за весь период эксплуатации преданную ему форму при изготовлении то оно является?
| 1.3
| Устойчивым
| Безразличным
| Не устойчивым
| Не растягиваться
| Не сжимающиеся
|
|
|
| Каким являются силы избражённые на рисунке?
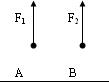
| 1.3
| Параллельными
| Антипараллельными
| Пара сил
| Две силы, направленные в одну сторону
| Направленные по разным линиям действия
|
|
|
| Как определить плечо пары:
| 1.2
| Кратчайшее расстояние между линия -ми действия двух сил
| Сложить силы
| Умножить одну силу на вторую
| Расстояние от начала одной силы до конца второй
| Расстояниек от начала до конца одной силы
|
|
|
| Как определить плечо силы относительно т.о

| 1.2
| Отпустить перпендикуляр из т.О на линию действия силы F
| Соеденить т А с точкой О
| Соединить т.ОС с точкой В.
| Разделить отрезок АВ на расстояние ОА
| Умножить АВ на расстояние ОА
|
|
|
|  Укажите где правильно составлено уранение равновесия:∑MB? Укажите где правильно составлено уранение равновесия:∑MB? 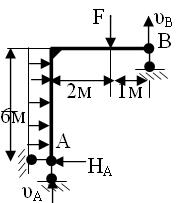
| 1.3
| ∑МВ=υА*3+
НА*6-q*6*3-F*1=0
| ∑МВ=υА –F*1-q*6*3=0
| ∑МВ=-υB*6+
НА*6-q*6*3-P*1=0
| ∑МВ=υА*4+
F*3-υA*4=0
| ∑МВ=υА*3+
НА*6-q*6-F*1=0
|
|
|
|    Укажите где правильно составлено уравнение равновесия ∑МА? Укажите где правильно составлено уравнение равновесия ∑МА? 
| 1.3
| ∑МA=F*6-q*4*2-MR=0
| ∑МA=F*1-q*4*2-MR=0
| ∑МA=F*4-q*4*2+υA-MR=0
| ∑МA=F*5-q*4*3-MR=0
| ∑МA=F*4+υA*5-q*4*2-MR=0
|
|
|
| Центр тяжести - сила или точка?
| 1.4
| Точка, через которую проходит сила тяжести при любом положении тела в пространстве
| Сила тяжести
| Точка, находящаяся вне тела
| Скорее всего сила, чем точка
| Скорее всего точка, чем сила
|
|
|
| Если сила пересекает ось в пространстве, то чему будет равен момент силы относительно этой оси?
| 1.4
| Нулю, т.к. плечо h равно нулю
| Равен произведению силы на плечо
| Момент будет отрицательным
| Момент будет положительным
| Момент будет нейтральным
|
|
|
| Если сила параллельна оси в пространстве, то чему будет равен момент этой силы относительно оси?
| 1.4
| Равен нулю, т.к. проекция силы на плоскость перпендикулярна оси равна нулю
| Равен произведению силы на плечо
| Момент будет отрицательным
| Момент будет положительным
| Момент будет нейтральным
|
|
|
| Если сила перпендикулярна к оси в пространстве, но не пересекает её, как определить момент силы относительно этой оси?
| 1.4
| Нужно умножить силу на её расстояние от оси
| Нужно удвоить силу
| Нужно умножить силу на ее длину
| Момент равен нулю
| Момент положительный
|
|
|
| Чему равна проекция силы F на ось Х-?

| 1.4
| Равны нулю
| Равна самой силе
| Равна удвоенной силе
| X=Fcos900
| X=Fsin900
|
|
|
| Чему равна проекция силы F на ось Х-?

| 1.4
| Проекция равна самой силе X=F
| X=0
| X=F*cos00
| X=F*sin00
| X=2F
|
|
|
| Чему равна проекция силы F на ось Х 
| 1.4
| F=cosά
| F=sinά
| X=0
| X=2F
| X=Ftgά
|
|
|
| Чему равна проекция силы F на ось Х-? 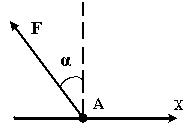
| 1.4
| Х=Fcosά
| Х=Fsinά
| Х=-Fcosά
| Х=Ftgsά
| Х=Fctgsά
|
|
|
| Если заданы 3 параллельные силы на плоскости и известны координаты их точек приложения в выбранной системе координат, то как определить координаты центра параллельных сил?
| 1.4
|  
| 
|  YE=0 YE=0
| XC=0 
|  
|
|
|
| Спроецировать силу на ось Х и У
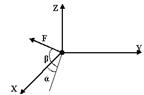
| 1.3
| FX=Fcosβ*cosά FY=Fcosβ*sinά
| FY=FX=Fcosβ
| FY=FX=Fsinά
| FX=Fsinά
FY=Fcosβ
| FY=Fsinά
FX=Fcosβ
|
|
|
| Спроецировать силу, лещащую в плоскости ZOY на ось Х

| 1.3
| FX=0
| FX=Fcosά
| FX=Fsinά
| FX=2F
| FX=Ftgά
|
|
|
| Спроецировать силу, лещащую в плоскости XOY на ось Z
| 1.3
| FZ=0
| FZ=Fsinά
| FZ=Fcosά
| FZ=Ftgά
| FZ=Fctgά
|
|
|
| Определить проекции заданной силы на оси Х,Y,Z
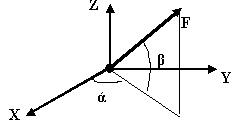
| 1.3
| FX=Fcosβ*cosά FY=Fcosβ*sinά FZ=Fsinβ
| FX=F*cosά
FY=F*sinά
FZ=Fsinβ
| FX=F*sinά
FY=F*cosά
FZ=Fcosβ
| FX=Fcosβ FY=Fcosβ
FZ=Fsinβ
| FX=F*cosά
FY=F*sinά
FZ=Fcosβ
|
|
|
| Спроецировать силу? Лежащую в плоскости XOZ на оси У

| 1.3
|

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Внешняя политика России 1894- 1917 гг. Внешнюю политику Николая II и первый период его царствования определяли, по меньшей мере три важных фактора...
Оценка качества Анализ документации. Имеющийся рецепт, паспорт письменного контроля и номер лекарственной формы соответствуют друг другу. Ингредиенты совместимы, расчеты сделаны верно, паспорт письменного контроля выписан верно. Правильность упаковки и оформления....
БИОХИМИЯ ТКАНЕЙ ЗУБА В составе зуба выделяют минерализованные и неминерализованные ткани...
|
Различие эмпиризма и рационализма Родоначальником эмпиризма стал английский философ Ф. Бэкон. Основной тезис эмпиризма гласит: в разуме нет ничего такого...
Индекс гингивита (PMA) (Schour, Massler, 1948) Для оценки тяжести гингивита (а в последующем и регистрации динамики процесса) используют папиллярно-маргинально-альвеолярный индекс (РМА)...
Методика исследования периферических лимфатических узлов. Исследование периферических лимфатических узлов производится с помощью осмотра и пальпации...
|




 b F2 с
F3
b F2 с
F3

 F1 R d
a
F1 R d
a

 b
b 

 F1 F2 с
F1 F2 с
 R F3
d
R F3
d



 F2 F3
F2 F3
 b
R d
F1
a
b
R d
F1
a 
 b
F1
b
F1

 a F3 c
a F3 c
 R
F2
d
R
F2
d

 R F1
c
R F1
c


























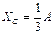
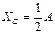

















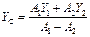




















 Укажите где правильно составлено уранение равновесия:∑MB?
Укажите где правильно составлено уранение равновесия:∑MB? 


 Укажите где правильно составлено уравнение равновесия ∑МА?
Укажите где правильно составлено уравнение равновесия ∑МА? 







 YE=0
YE=0










