Раскрыть основные этапы работы по развитию и форимированию понятия «величина» в курсе начальной математики.

Понятие величины является важнейшим понятием математики. Каждая изучаемая величина – это некоторое свойство реальных объектов окружающего мира. Учащиеся должны получать конкретные представления об этих величинах, ознакомиться с еденицами их измерения, овладеть умениями измерять величины, выражать результаты измерения.

Длина отрезка: с первых дней в школе дети выделяют расстояние (длину, ширину, высоту предметов, расстояние между ними). Важнейшим шагом является знакомство с прямой линией и отрезком.

Первой величиной вводится сантиметр. На уроках советуют пользоваться линейками которые дети изготовили сами. При работе с линейкой необходимо обратить внимание на начало отрезка, которое равно нулю на линейке.

Введение миллиметра обуславливается необходимостью измерять отрезки меньше 1 сантиметра. Наглядное представление дети получают, рассматривая деления на линейке. При введении километра полезно провести практические занятия на местности.

Площадь геометрических фигур: в процессе изучения геометрического материала уточняется представление о площади как о свойстве плоских фигур. Дети узнают что при изменении положения фигур площадь не меняется.. Единицей площади является 1 ^{2 .} Фигуры которые не делятся на квадратный сантиметр используют палетку.

Масса: сильное влияние на оценку предмета оказывает размер предмета. Дети могут определить примерную массу предмета «на руку». Введение килограма учитель показывает пример на весах.

Время: вся жизнь человека тесно связана со временем, с умением измерять, распределять,ценитьвремя. Время течёт беспрерывно его нельзя ни остановить, ни возвратить.Время – одна из трудных для изучения величин. Неопходимо научить детей пользоваться календарём, часами.При изучении виличин меесяц и год учитель использует календарь. А при изучении суток расскрывается через близкие детям понятия о частях суток: утро, день, вечер, ночь. И с помощью временной последовательности: вчера, сегодня, завтра. Введение часа, минуты осуществляют с помощью отношения между мерами времени: 1 сутки-это 24часа, 1час это 60минут и т. д. Чтобы дети научились правильно устанавливать время по часам полезно заготовить циферблат с подвижными стрелкам

 

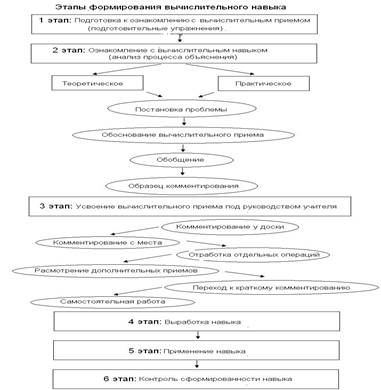
8. По определению дробь - это число вида m / n, где т и п — целые числа, причем п не равно 0.

Далее определяется ряд операций для чисел этого вида (что понимать под сложением и вычитанием дробей, что понимать под умножением и делением дробей, какую дробь считать большей, а какую – меньшей). Определяется ряд свойств, которыми обладают дроби (например, основное свойство дроби: числитель и знаменатель можно умножить или разделить на одно и то же число, при этом значение дроби не изменится). В учебниках математики для начальных классов отражен другой подход к определению понятия рационального числа (дроби) - через измерение длины отрезка. Для описания результата этого процесса используют дробь.

Программой начальных классов не предусмотрено формирование понятия дроби как числа. Сведения о дробях ребенок получает только через практические действия над реальными объектами, величинами, множествами и описание этих действий на языке специальных символов (дробей). Все эти действия считаются подготовкой к знакомству с дробями в 5 - 6 классе. Данный подход к формированию представлений о долях и дробях реализован во всех альтернативных учебниках математики для начальных классов.

Методическая проблема знакомства ребенка с дробями состоит в выборе учителем целесообразного множества исходных объектов и практических операций, которые ученик будет выполнять над ними. Понятие дроби будет отождествляться с результатом этой операции. Термин «целесообразное множество» подразумевает, что множество выбранных объектов должно делиться нацело, при этом в случае геометрической фигуры можно иметь в виду и равновеликие части.

Сформированность представлений о дробях отражается в умении выполнять следующие операции:

1) записывать дробь, ориентируясь на объект или рисунок;

2) сравнивать дроби с опорой на объект или рисунок;

3) находить «дробь от числа» (делением объекта или множества на равные части);

4) восстанавливать число по известной его дроби (обратная операция).

Все эти умения формируются на основе принципа наглядности и неотрывности от предметного содержания.

Словом «доля» в 3 классе называют дробь вида 1 / k. Долю получают делением объекта на несколько равных частей.

Запись вида 1 / 2 подразумевает, что объект разделили на две равных части и взяли одну из них. Запись такого вида в последней редакции учебника математики для 3 класса традиционной программы не рассматривается.

Детям сообщается словесное название полученной части: одна двенадцатая доля, одна шестая доля и т. д.

Используя рисунок круга, разделенного на равные части, дети сравнивают доли, обозначая результат сравнения словом (а не знаком). Например: «Назови, какие доли круга получились на каждом рисунке. Сравни, какая доля больше: одна восьмая или одна четвертая; одна третья или одна шестая?».

После этого в учебнике сразу предлагаются задания на нахождение доли величины и величины по ее доле, сформулированные в виде задач.

Приведем пример задания на нахождение доли величины:

«Длина ленты 9 см. Отрезали одну треть этой ленты. Сколько дециметров ленты отрезали?»

Выполнение:

Данное задание является типовой задачей на нахождение доли величины. Смысл задания соответствует процессу нахождения доли объекта. Для иллюстрации этого смысла ученики чертят в тетради отрезок длиной 9 см (модель заданного в задаче объекта). Повторяют способ действия для получения одной третьей части (доли) объекта: разделим отрезок на три равные части. Запись 9 см: 3 = 3 см. Затем (проверка) выполняют операцию разделения на отрезке и измеряют полученную третью часть.

10. Вычислительный навык - это высокая степень овладения вычислительными приемами, можно сделать вывод, что приобрести вычислительные навыки - это значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнить необходимые операции достаточно быстро. Полный вычислителей навык характеризуется следующими качествами: правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом, точностью и скоростью.

Формирование вычислительного навыка, обладающего названными качествами, обеспечивается построением начального курса математики и использованием соответствующих вычислительных приемов.

Прием вычисления над данными числами складывается из ряда последовательных операций (системы операций), выполнение которых приводит к нахождению результата требуемого арифметического действия над этими числами. Причем выбор операций в каждом приеме определяется теми арифметическими положениями, которые используются в качестве его теоретической основы.

Формирование любого вычислительного навыка проходит одни и те же этапы (см. таблицу).

 

 

В методике преподавания математики выделены следующие группы вычислений:

Навыки письменных вычислений. Результат этих вычислений находится с помощью специальных приемов для письменных вычислений

При введении большинства вычислительных приемов целесообразно использовать наглядность. Для приемов первой группы - оперирование множествами. Например, прибавляя к 7 число 2. придвигаем к 7 квадратам (кружкам и т.п.) 2 квадрата (кружка и т.п.) по одному. В ходе работы над приемами второй группы в качестве наглядности используется развернутая запись всех операций. Например, при введении приема внетабличного умножения выполняется такая запись: 14 • 5 = (10 + 4) • 5 = 10 • 5 + 4 • 5 = 70. В ряде случаев наряду с ней используется и оперирование множествами (например, при ознакомлении с приемами сложения и вычитания в пределах 100). Выполнение каждой операции важно сопровождать устными пояснениями. Сначала они производятся под руководством учителя, а затем учащиеся делают это самостоятельно. В пояснении указывается, какие необходимы операции, каков их порядок; называется результат каждой из них. При этом не раскрываются ранее изученные приемы, входящие в качестве операции в новом приеме (основные операции). Например, прибавляя к 7 число 2, ученик так поясняет выполнение операций: «К семи прибавлю 1, получится 8; к 8 прибавлю 1, получится 9» (как прибавить 1 - не поясняется). При умножении чисел 14 и 5 пояснение будет следующим: заменю число 14 суммой разрядных слагаемых 10 и 4, получу пример: сумму чисел 10 и 4 умножить на 5. Умножим на 5 первое слагаемое - 10, получится 50, умножим на 5 второе слагаемое - 4, получится 20, сложим результаты 50 и 20, получится 70 (здесь не поясняется, как умножить 10 на 5, как умножить 4 на 5 и как сложить 50 и 20).