Для расчета аэродинамического нагрева необходимо знать параметры газа на внешней границе пограничного слоя обтекаемого тела - 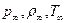 . То есть необходимо иметь результаты расчета обтекания тела без учета наличия пограничного слоя по заданным форме тела, его размеров, траектории движения и параметров воздуха по этой траектории.
. То есть необходимо иметь результаты расчета обтекания тела без учета наличия пограничного слоя по заданным форме тела, его размеров, траектории движения и параметров воздуха по этой траектории.
Рассмотрим теплообмен в окрестности критической точки притупленного тела. При гиперзвуковых скоростях давление газа в критической точке мало отличается от давления за прямым скачком уплотнения. Следовательно, для нахождения давления в критической точке достаточно определить параметры потока за прямым скачком уплотнения. При этом используются уравнения, выражающие законы сохранения импульса и энергии при переходе через прямой скачок уплотнения, а также уравнение неразрывности:
 ;
;  ;
; 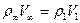
Зная давление за скачком уплотнения, можно оценить величину 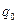 плотности теплового потока, подводимого к поверхности затупленного тела в окрестности точки торможения, используя формулы из работы Фенстера [ 13 ], которые получены им в результате аппроксимации расчетных зависимостей
плотности теплового потока, подводимого к поверхности затупленного тела в окрестности точки торможения, используя формулы из работы Фенстера [ 13 ], которые получены им в результате аппроксимации расчетных зависимостей 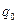 от
от  ,
, 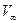 и радиуса
и радиуса 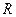 затупления тела. В отмеченной работе Фенстер приводит аппроксимационные зависимости для случая замороженного и равновесного пограничного слоя. Для замороженного случая зависимость имеет вид:
затупления тела. В отмеченной работе Фенстер приводит аппроксимационные зависимости для случая замороженного и равновесного пограничного слоя. Для замороженного случая зависимость имеет вид: 
 ,
,
а для равновесного - 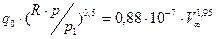 .
.
В представленных соотношениях  - давление на уровне моря, размерность
- давление на уровне моря, размерность 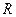 -
- 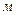 ,
, 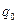 -
-  ,
, 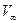 -
-  ,
, 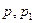 -
-  . В отмеченной работе показано, что экспериментальные данные заполняют все пространство между расчетными кривыми, полученными для случая замороженного и равновесного пограничных слоев. Это демонстрируется на приведенном ниже рисунке, заимствованном из работы Фенстера.
. В отмеченной работе показано, что экспериментальные данные заполняют все пространство между расчетными кривыми, полученными для случая замороженного и равновесного пограничных слоев. Это демонстрируется на приведенном ниже рисунке, заимствованном из работы Фенстера.
В инженерной практике для определения плотности теплового потока  , подводимого к поверхности тела, обтекаемого высокотемпературным газом, широко используется модификация формулы Ньютона
, подводимого к поверхности тела, обтекаемого высокотемпературным газом, широко используется модификация формулы Ньютона  , где
, где  - коэффициент теплоотдачи от газа к неразрущающейся и нереагирующей стенке обтекаемого тела,
- коэффициент теплоотдачи от газа к неразрущающейся и нереагирующей стенке обтекаемого тела,  и
и 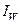 - соответственно эффективная энтальпия газа на границе пограничного слоя и действительная энтальпия газа у стенки. При этом для лобовой части
- соответственно эффективная энтальпия газа на границе пограничного слоя и действительная энтальпия газа у стенки. При этом для лобовой части  ,
, 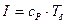 . Для других частей обтекаемого тела эффективная энтальпия несколько меньше энтальпии полностью заторможенного потока. Использование для определения
. Для других частей обтекаемого тела эффективная энтальпия несколько меньше энтальпии полностью заторможенного потока. Использование для определения  разности
разности  позволяет учесть перенос химической энергии, которая выделяется за счет рекомбинации диссоциированных молекул при их диффузии поперек пограничного слоя к поверхности тела. Что касается коэффициента
позволяет учесть перенос химической энергии, которая выделяется за счет рекомбинации диссоциированных молекул при их диффузии поперек пограничного слоя к поверхности тела. Что касается коэффициента  , то он определяется с помощью известных в теории конвективного теплообмена критериальных зависимостей. В монографии [13]
, то он определяется с помощью известных в теории конвективного теплообмена критериальных зависимостей. В монографии [13]  рекомендуется определять с помощью приведенных ниже формул, полученных из критериальных соотношений для сравнительно малых скоростей.
рекомендуется определять с помощью приведенных ниже формул, полученных из критериальных соотношений для сравнительно малых скоростей.
Для ламинарного пограничного слоя  ;
;
для турбулентного пограничного слоя  .
.
Расчеты и экспериментальные исследования показали, что приведенные выражения для коэффициента  можно использовать и для случая гиперзвуковых скоростей, если ввести в эти выражения поправочные множители, учитывающие переменность
можно использовать и для случая гиперзвуковых скоростей, если ввести в эти выражения поправочные множители, учитывающие переменность  и
и  поперек пограничного слоя, наличие химических реакций в пограничном слое, вдув продуктов разложения стенки в пограничный слой.
поперек пограничного слоя, наличие химических реакций в пограничном слое, вдув продуктов разложения стенки в пограничный слой.
Из аппроксимационных зависимостей Фенстера следует, что в окрестности точки торможения 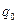 пропорционален величине выражения
пропорционален величине выражения  . Отсюда следует, что путем увеличения радиуса затупления носовой части тела можно уменьшить конвективный теплообмен в этой области.
. Отсюда следует, что путем увеличения радиуса затупления носовой части тела можно уменьшить конвективный теплообмен в этой области.
Расчет распределения плотности тепловых потоков по поверхности тела является более сложной задачей, чем анализ теплообмена в окрестности точки торможения. В [13] для случая обтекания сферы равновесно диссоциированным гиперзвуковым потоком воздуха и при отсутствии излучения приводится простая зависимость, достаточно хорошо описывающая распределение теплового потока по поверхности сферы:
 ,
,
где  - угол между осью симметрии тела и радиусом – вектором рассматриваемой точки.
- угол между осью симметрии тела и радиусом – вектором рассматриваемой точки.
Как уже отмечалось увеличение радиуса затупления тела приводит к снижению конвективного теплового потока. Однако большой радиус затупления может вызвать появление за ударной волной значительных по толщине сжатых слоев высокотемпературного излучающего газа. В [1] на основе результатов расчета толщины ударного слоя и результатов расчета зависимости излучательной способности этого слоя от параметров набегающего потока воздуха получены выражения для плотности радиационного теплового потока 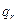 к поверхности спускаемого аппарата от оптически прозрачного ударного слоя с постоянными параметрами:
к поверхности спускаемого аппарата от оптически прозрачного ударного слоя с постоянными параметрами:
1) 
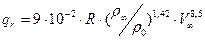 ;
;
2) 
 ;
;
3) 
 ,
,
где  - плотность воздуха при нормальных условиях (
- плотность воздуха при нормальных условиях ( ),
), 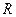 - радиус кривизны поверхности лобовой части спускаемого аппарата.
- радиус кривизны поверхности лобовой части спускаемого аппарата.
Конвективный и радиационный тепловые потоки неодинаково зависят от скорости полета. Если при  радиационный тепловой поток к поверхности СА пренебрежимо мал по сравнению с конвективным даже при больших значениях
радиационный тепловой поток к поверхности СА пренебрежимо мал по сравнению с конвективным даже при больших значениях 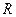 (порядка
(порядка  ), то по мере возрастания
), то по мере возрастания 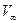 соотношение между конвективным и радиационным тепловыми потоками меняется в сторону относительного увеличения
соотношение между конвективным и радиационным тепловыми потоками меняется в сторону относительного увеличения 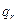 . При высоких скоростях полета затупленного тела радиационный тепловой поток к его поверхности становится доминирующим в тепловом балансе. Разумеется, многое зависит и от радиуса затупления, поскольку с уменьшением
. При высоких скоростях полета затупленного тела радиационный тепловой поток к его поверхности становится доминирующим в тепловом балансе. Разумеется, многое зависит и от радиуса затупления, поскольку с уменьшением 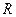
 радиационный тепловой поток должен уменьшаться пропорционально уменьшению толщины ударного слоя. В монографиях [7,14] приводятся в виде графиков результаты сопоставления зависимости от скорости полета конвективного и радиационного потока при
радиационный тепловой поток должен уменьшаться пропорционально уменьшению толщины ударного слоя. В монографиях [7,14] приводятся в виде графиков результаты сопоставления зависимости от скорости полета конвективного и радиационного потока при  . Из этих графиков, копии которых представлены ниже на рисунке 2.6, следует, что расчетные значения сопоставляемых потоков соизмеримы при
. Из этих графиков, копии которых представлены ниже на рисунке 2.6, следует, что расчетные значения сопоставляемых потоков соизмеримы при  , а при скорости выше
, а при скорости выше 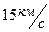 радиационный тепловой поток превышает конвективный в 10 раз и более.
радиационный тепловой поток превышает конвективный в 10 раз и более.
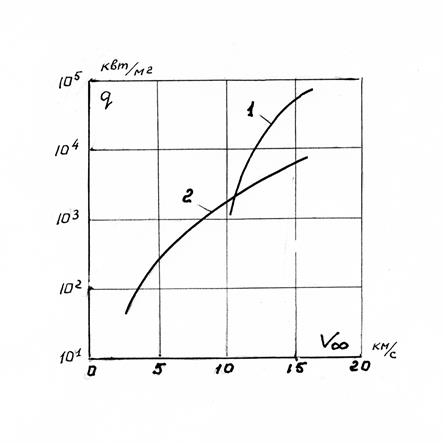
Рис.2.6. Сравнение радиационного (1) и конвективного (2) тепловых потоков в точке торможения затупленного тела с радиусом  при различных скоростях полета
при различных скоростях полета 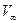

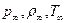 . То есть необходимо иметь результаты расчета обтекания тела без учета наличия пограничного слоя по заданным форме тела, его размеров, траектории движения и параметров воздуха по этой траектории.
. То есть необходимо иметь результаты расчета обтекания тела без учета наличия пограничного слоя по заданным форме тела, его размеров, траектории движения и параметров воздуха по этой траектории. ;
;  ;
; 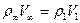
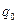 плотности теплового потока, подводимого к поверхности затупленного тела в окрестности точки торможения, используя формулы из работы Фенстера [ 13 ], которые получены им в результате аппроксимации расчетных зависимостей
плотности теплового потока, подводимого к поверхности затупленного тела в окрестности точки торможения, используя формулы из работы Фенстера [ 13 ], которые получены им в результате аппроксимации расчетных зависимостей  ,
, 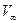 и радиуса
и радиуса 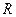 затупления тела. В отмеченной работе Фенстер приводит аппроксимационные зависимости для случая замороженного и равновесного пограничного слоя. Для замороженного случая зависимость имеет вид:
затупления тела. В отмеченной работе Фенстер приводит аппроксимационные зависимости для случая замороженного и равновесного пограничного слоя. Для замороженного случая зависимость имеет вид: 
 ,
,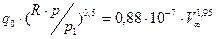 .
. - давление на уровне моря, размерность
- давление на уровне моря, размерность 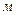 ,
,  ,
,  ,
, 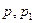 -
-  . В отмеченной работе показано, что экспериментальные данные заполняют все пространство между расчетными кривыми, полученными для случая замороженного и равновесного пограничных слоев. Это демонстрируется на приведенном ниже рисунке, заимствованном из работы Фенстера.
. В отмеченной работе показано, что экспериментальные данные заполняют все пространство между расчетными кривыми, полученными для случая замороженного и равновесного пограничных слоев. Это демонстрируется на приведенном ниже рисунке, заимствованном из работы Фенстера. , подводимого к поверхности тела, обтекаемого высокотемпературным газом, широко используется модификация формулы Ньютона
, подводимого к поверхности тела, обтекаемого высокотемпературным газом, широко используется модификация формулы Ньютона  , где
, где  - коэффициент теплоотдачи от газа к неразрущающейся и нереагирующей стенке обтекаемого тела,
- коэффициент теплоотдачи от газа к неразрущающейся и нереагирующей стенке обтекаемого тела,  и
и 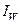 - соответственно эффективная энтальпия газа на границе пограничного слоя и действительная энтальпия газа у стенки. При этом для лобовой части
- соответственно эффективная энтальпия газа на границе пограничного слоя и действительная энтальпия газа у стенки. При этом для лобовой части  ,
, 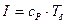 . Для других частей обтекаемого тела эффективная энтальпия несколько меньше энтальпии полностью заторможенного потока. Использование для определения
. Для других частей обтекаемого тела эффективная энтальпия несколько меньше энтальпии полностью заторможенного потока. Использование для определения  позволяет учесть перенос химической энергии, которая выделяется за счет рекомбинации диссоциированных молекул при их диффузии поперек пограничного слоя к поверхности тела. Что касается коэффициента
позволяет учесть перенос химической энергии, которая выделяется за счет рекомбинации диссоциированных молекул при их диффузии поперек пограничного слоя к поверхности тела. Что касается коэффициента  , то он определяется с помощью известных в теории конвективного теплообмена критериальных зависимостей. В монографии [13]
, то он определяется с помощью известных в теории конвективного теплообмена критериальных зависимостей. В монографии [13]  рекомендуется определять с помощью приведенных ниже формул, полученных из критериальных соотношений для сравнительно малых скоростей.
рекомендуется определять с помощью приведенных ниже формул, полученных из критериальных соотношений для сравнительно малых скоростей. ;
; .
. и
и  поперек пограничного слоя, наличие химических реакций в пограничном слое, вдув продуктов разложения стенки в пограничный слой.
поперек пограничного слоя, наличие химических реакций в пограничном слое, вдув продуктов разложения стенки в пограничный слой. . Отсюда следует, что путем увеличения радиуса затупления носовой части тела можно уменьшить конвективный теплообмен в этой области.
. Отсюда следует, что путем увеличения радиуса затупления носовой части тела можно уменьшить конвективный теплообмен в этой области. ,
, - угол между осью симметрии тела и радиусом – вектором рассматриваемой точки.
- угол между осью симметрии тела и радиусом – вектором рассматриваемой точки.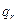 к поверхности спускаемого аппарата от оптически прозрачного ударного слоя с постоянными параметрами:
к поверхности спускаемого аппарата от оптически прозрачного ударного слоя с постоянными параметрами:
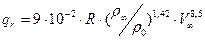 ;
;
 ;
;
 ,
, - плотность воздуха при нормальных условиях (
- плотность воздуха при нормальных условиях ( ),
),  радиационный тепловой поток к поверхности СА пренебрежимо мал по сравнению с конвективным даже при больших значениях
радиационный тепловой поток к поверхности СА пренебрежимо мал по сравнению с конвективным даже при больших значениях  ), то по мере возрастания
), то по мере возрастания  радиационный тепловой поток должен уменьшаться пропорционально уменьшению толщины ударного слоя. В монографиях [7,14] приводятся в виде графиков результаты сопоставления зависимости от скорости полета конвективного и радиационного потока при
радиационный тепловой поток должен уменьшаться пропорционально уменьшению толщины ударного слоя. В монографиях [7,14] приводятся в виде графиков результаты сопоставления зависимости от скорости полета конвективного и радиационного потока при  . Из этих графиков, копии которых представлены ниже на рисунке 2.6, следует, что расчетные значения сопоставляемых потоков соизмеримы при
. Из этих графиков, копии которых представлены ниже на рисунке 2.6, следует, что расчетные значения сопоставляемых потоков соизмеримы при  , а при скорости выше
, а при скорости выше 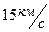 радиационный тепловой поток превышает конвективный в 10 раз и более.
радиационный тепловой поток превышает конвективный в 10 раз и более.



