Теоремы сложения вероятностей
Теорема. Вероятность появления хотя бы одного из двух Р(А+В) = Р(А) + Р(В) – Р(AB). Теорема (для несовместных событий). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
✓ Теорема справедлива для любого конечного числа несовместных событий A1, A2, …, An:
Из этой теоремы следует формула для противоположных событий A и Р(А)+Р( Пример. На стеллаже в библиотеке в случайном порядке Решение (первый способ). Требование - хотя бы один из Интересующее нас событие А можно представить в виде суммы событий: А=A+C+D. По теореме сложения, Р(А) =Р(В) +Р(С) +P(D) (1) Найдем вероятности событий В, С и D.
Подставив эти вероятности в формулу (1) окончательно получим: Р(А)=45/91+20/91+2/91=67/91. Решение (второй способ). События А (хотя бы один из взятых трех учебников имеет переплет) и
|


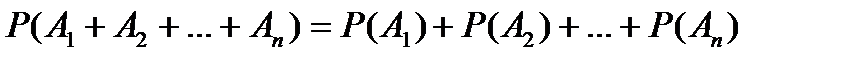
 :
: ) = 1
) = 1


 = 1 - 24/91= 67/91
= 1 - 24/91= 67/91


