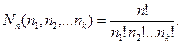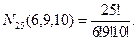Разбиение множества на группы

Если множество из n различных элементов разбивается на k групп так, что в первую группу попадают n₁ элементов, во вторую – n₂ элементов, в k-ую группу – n_k элементов, причем n₁+n₂+...+n_k=n, то число таких разбиений равно

Задача 9. Сколькими способами можно разбить группу из 25 студентов на три подгруппы по 6, 9 и 10 человек в каждой группе?

Решение. Здесь n=25, k=3, n₁=6, n₂=9, n₃=10. Согласно формуле, число таких разбиение равно

Задача 10. Сколько существует семизначных чисел, состоящих из цифр 4,5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 - по 2 раза?

Решение. Каждое семизначное число отличается от другого порядком следования цифр, при этом фактически все семь мест в этом числе делятся на три группы: на одни места ставится цифра «4», на другие места – цифра «5», а на третьи места – цифра «6». Таким образом, в нашем случае множество состоит из 7 элементов (n=7), причем n₁=3, n₂=2, n₃=2), и, следовательно, в силу формулы число таких чисел равно

 

Задачи для самостоятельного решения

1. В ящике 5 красных и 4 зеленых яблока. Сколькими способами можно выбрать три яблока из ящика?

2. Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?

3. Сколькими способами можно вытащить две карты пиковой масти из колоды в 36 карт?

4. Десять человек при встрече обмениваются рукопожатиями. Сколько всего рукопожатий будет сделано?

5. Доступ к файлу открывается только если введен правильный пароль – определенный трехзначный номер из пяти цифр. Каково максимальное число возможных попыток угадать пароль?

6. Сколькими способами можно расположить на шахматной доске две ладьи так, одна не могла взять другую? (Одна ладья может взять другую, если она находится с ней на одной горизонтали или на одной вертикали шахматной доски).

7. Сколькими способами можно расположить на полке 10 томов энциклопедии?

8. Сколькими способами можно расположить на полке 10 томов энциклопедии так, чтобы девятый и десятый тома рядом не стояли?

9. Группу из 10 человек требуется разбить на две непустые подгруппы. Сколькими способами это можно сделать?

10. Группу из 10 человек требуется разбить на две подгруппы так, чтобы в первой группе было 6 человек, а во второй – 4 человека. Сколькими способами это можно сделать?

11. Группу из 16 человек требуется разбить на 3 подгруппы, в первой из которых должно быть 5 человек, во второй — 7 человек, в третьей — 4 человека. Сколькими способами это можно сделать?

12. Сколько существует двухзначных чисел, кратных либо 2, либо 5, либо тому и другому числу одновременно?

13. Из бригады в 14 врачей человек ежедневно в течении 7 дней назначают двух дежурных врачей. Определить количество различных расписаний дежурства, если каждый человек дежурит один раз?

14. Сколько четырехзначных чисел, составленных из нечетных цифр, содержит цифру 3 (цифры в числах не повторяются)?

15. Шесть групп занимаются в 6 расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях?

16. Восемь мешков постельного белья доставляются на пять этажей гостиницы. Сколькими способами можно распределить мешки по этажам? В скольких вариантах на пятый этаж доставлен один мешок?

17. Два наборщика должны набрать 16 текстов. Сколькими способами они могут распределить эту работу между собой?

18. Поезд метро делает 16 остановок, на которых выходят пассажиры. Сколькими способами могут распределиться между этими остановками 100 пассажиров, вошедших в поезд на конечной остановке?

19. Акционерное собрание компании выбирает из 50 человек президента компании, председателя совета директоров и 10 членов совета директоров. Сколькими способами можно это сделать?

20. Из фирмы, в которой работают 10 человек, 5 сотрудников должны уехать в командировку. Сколько может быть составов этой группы, если директор фирмы, его заместитель и главный бухгалтер одновременно уезжать не должны?

21. В телевизионной студии работают 3 режиссера, 4 звукорежиссера, 5 операторов, 7 корреспондентов и 2 музыкальных редактора. Сколькими способами можно составить съемочную группу, состоящую из одного режиссера, двух операторов, одного звукорежиссера и двух корреспондентов?

22. Из группы в 25 человек должны быть выделены староста и 3 члена студкома. Сколькими способами это можно сделать?

23. Шесть студентов-переводников следует распределить по трем группам второго курса. Сколькими способами это можно сделать?

24. Лифт останавливается на 7 этажах. Сколькими способами могут распределиться между этими этажами 6 пассажиров, находящихся в кабине лифта?

25. Восемь авторов должны написать книгу из 16 глав. Сколькими способами можно распределить материал между авторами, если два человека напишут по три главы, четыре - по две и два - по одной главе книги?

26. Из цифр 1,2,3,4,5,6,7,8,9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.

27. Сколько существует пятизначных телефонных номеров, в которых есть цифры 1 и 2?

28. Семь яблок и три апельсина надо положить в два пакета так, чтобы в каждом пакете был хотя бы один апельсин и чтобы количество фруктов в них было одинаковым. Сколькими способами это можно сделать?

29. Байт – это слово, состоящее из восьми бит, каждый бит равен либо 0, либо 1. Сколько символов можно закодировать с помощью байтов?

30. Автомобильный номер состоит из трех букв и трех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?

31. Садовник должен в течении трех дней посадить 10 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?

32. Из ящика, в котором лежат 10 красных и 5 зеленых яблока, выбирают одно красное и два зеленых яблока. Сколькими способами это можно сделать?

33. Десяти ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?

34. Студенческую группу в 24 человек (12 девушек и 12 юношей), разбивают на две равные подгруппы так, чтобы в каждой подгруппе юношей и девушек было поровну. Сколькими способами это можно сделать?

35. Группа, состоящая из 25 человек, пишет контрольную работу, в которой три варианта. Сколькими способами можно выбрать 5 человек из группы так, чтобы среди них оказались писавшие все три варианта?

36. Лифт, в котором находится 9 пассажиров, может останавливаться на 10 этажах. Пассажиры выходят группами по два, по три и четыре человека. Сколькими способами это может произойти?

37. Сколькими способами можно расставить группу из 10 человек в очередь так, чтобы между двумя студентами А. и Б. было два человека?

38. Есть 3 билета в различные театры. Сколькими способами они могут быть распределены среди 25 студентов группы, если каждый студент может получить только один билет?

39. На группу из 25 человек выделены 3 пригласительных билета на вечер. Сколькими способами они могут быть распределены (не более одного билета в руки)?

40. Имеются 7 билетов: 3 в один театр и 4 — в другой. Сколькими способами они могут быть распределены между студентами группы из 25 человек?