Основные правила комбинаторики
Дифференциальное уравнение изгиба круглых пластин при действии произвольной поперечной нагрузки:
В случае осесимметричного нагружения
Решение основного уравнения имеет вид:
Для нахождения произвольных постоянных (констант) используем граничные условия.
В заделке:
На свободном крае:
В результате получим систему четырех алгебраических уравнений для нахождения четырёх констант С1, С2, С3, С4:
Далее, определяем произвольные постоянные и подставляем их в формулы (*), по которым строим графики.
Часть I. Случайные события. Глава 1. Элементы комбинаторного анализа. Одной из основных задач комбинаторики является подсчет числа элементов конечных множеств, заданных каким-либо дескриптивным условием. Рассмотрим типовые ситуации.
Основные правила комбинаторики Пусть имеется k групп А1,А2,...,Аk, причем i-ая группа содержит ni элементов. Тогда: А. Правило умножения (основная теорема комбинаторики). Общее число N способов, которыми можно получить упорядоченную совокупность (a1,a2,...ak), где aiÎAi (т.е. выбрать по одному элементу из каждой группы и расставить их в определенном порядке), равно
Б. Правило сложения. Если один элемент из группы Ai можно выбрать ni способами, и при этом любые две группы Ai и Aj не имеют обших элементов, то выбор одного элемента или из A1, или из A2,..., или из Ak можно осуществить
Задача 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать? Решение. Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом - любой из оставшихся 28 студентов, т.е. n1=30, n2=29, n3=28. По правилу умножения общее число N способов выбора старосты, его заместителя и профорга равно N=n1´n2´n3=30´29´28=24360.
Задача 2. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу? Решение. Первое письмо имеет n1=2 альтернативы – либо его относит к адресату первый почтальон, либо второй. Для второго письма также есть n2=2 альтернативы и т.д., т.е. n1=n2=…=n10=2. Следовательно, в силу правила умножения общее число способов распределений писем между двумя почтальонами равно
Задача 3. В ящике 100 деталей, из них 30 – деталей 1-го сорта, 50 – 2-го, остальные – 3-го. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта? Решение. Деталь 1-го сорта может быть извлечена n1=30 способами, 2-го сорта – n2=50 способами. По правилу суммы существует N=n1+n2=30+50=80 способов извлечения одной детали 1-го или 2-го сорта.
§ 2. Упорядоченные совокупности (последовательный выбор) Пусть имеется некоторая конечная совокупность элементов {a1,a2,...,an}, называемая генеральной совокупностью и n – объем этой совокупности. Пусть эксперимент состоит в том, что из генеральной совокупности последовательно выбирают k элементов и располагают их в порядке выбора. Возможны две ситуации.
А. Размещения без повторений. Отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется размещением k элементов из n, или последовательным выбором без возвращения. Итак, размещения – это упорядоченные совокупности k элементов из n, отличающиеся друг от друга либо составом, либо порядком элементов. Например. Пусть имеется множество Требуется найти число различных способов, которыми можно произвести последовательную выборку без возвращения k элементов из генеральной совокупности объема n. Очевидно, что первый элемент можно выбрать n1=n способами, и так как отобранный элемент не возвращается в генеральную совокупность, то следующий элемент выбирается из совокупности, объем которой на один элемент меньше, то есть n2=n-1, и т.д. так, что nk=n-(k-1). Тогда по правилу умножения общие число N способов равно N=n(n-1)...(n-(k-1)). Такое число обозначается
В частном случае, когда выбираются все элементы генеральной совокупности, т.е. когда k=n, размещения называются перестановками.
Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из n элементов обозначается
Например. Все перестановки множества
Б. Размещения с повторениями. Если каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность, то такой выбор называется размещением с повторениями (или последовательный выбор с возвращением). Так как на каждом шаге выборка производится из генеральной совокупности объема n, то общее число Пример. Все размещения с повторениями двух элементов из множества с тремя элементами
Задача 4. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин. Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и их порядком следования, поэтому Задача 5. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены различные премии? Решение. Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом, так и их порядком. Так как каждый фильм может получить призы как по одной, так и по нескольким номинациям, то одни и те же фильмы могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 10 элементов по5:
§ 3. Неупорядоченные совокупности (одновременный выбор) А. Сочетания без повторений. Если комбинации из n элементов по k отличаются только составом элементов, то их рассматривают как одновременный неупорядоченный выбор k элементов из генеральной совокупности объема n и называют сочетаниями из n элементов по k. То есть, сочетания – это неупорядоченные совокупности элементов, отличающиеся друг от друга только составом элементов. Например.Все сочетания без повторений двух элементов из множества
Формула для вычисления числа сочетаний n элементов по k:
Свойства числа сочетаний:
Б. Сочетания с повторениями. Если в сочетаниях из n элементов по k некоторые из элементов или все могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями из n элементов по k, и число сочетаний с повторениями из n элементов по k равно
Пример. Все сочетания с повторениями двух элементов из множества
Задача 6. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми участниками должна быть сыграна одна партия? Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2. Их число равно Задача 7. В условиях задачи 5 определить, сколько существует вариантов распределения призов, если по каждой номинации установлены одинаковые призы? Решение. Если по каждой номинации установлены одинаковые призы, то порядок фильмов в комбинации 5 призов значения не имеет, и число вариантов представляет собой число сочетаний с повторениями из 10 элементов по 5, определяемое по формуле Задача 8. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно? Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число равно
|


 уравнения принимают вид:
уравнения принимают вид:
 (*)
(*)


 .
. способами.
способами. .
. из трех элементов. Тогда все размещения двух элементов из трех таковы:
из трех элементов. Тогда все размещения двух элементов из трех таковы: 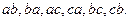
 , т.е.
, т.е. 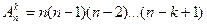 , или
, или .
. и вычисляется по формуле
и вычисляется по формуле .
. и
и 
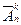 различных способов, какими можно произвести выборку с возвращением k элементов из генеральной совокупности объема n равно
различных способов, какими можно произвести выборку с возвращением k элементов из генеральной совокупности объема n равно  .
.













