КОНТРОЛЬНАЯ РАБОТА. В задаче 1 выполняется расчет параметров состояния смеси и процесса изменения состояния смеси идеальных газов с переменной теплоемкостью
В задаче 1 выполняется расчет параметров состояния смеси и процесса изменения состояния смеси идеальных газов с переменной теплоемкостью. Количество подведенной теплоты и изменение внутренней энергии и энтропии следует рассчитывать с использованием средних теплоемкостей смеси. Средние изобарная
где Средние теплоемкости смеси (изобарная и изохорная) определяются по формуле
где Далее теплота Q, работа L, изменение внутренней энергии DU, энтальпии DH и энтропии DS вычисляются следующим образом:
где m см – масса смеси. В задаче 2 выполняется расчет процессов изменения состояния водяного пара. Все параметры состояния пара определяются по h-s диаграмме водяного пара, а параметры в начальном состоянии (υ, h, s) дополнительно вычисляются и с использованием таблиц теплофизических свойств воды и водяного пара [5]. Скорость пара на выходе из сопла Лаваля определяется по формуле
В задаче 3 выполняется расчет основных параметров многоступенчатого поршневого компрессора с охлаждением газа при постоянном давлении после сжатия в каждой ступени. Отношение давления на выходе pвых и на входе pвх каждой ступени принимается одинаковым и определяется как
N = z m lк.ст, (8)
где m – массовый расход газа, кг/с; lк.ст – теоретическая работа, расходуемая на сжатие газа на каждой ступени, кДж/кг. Количество теплоты, отводимое от газа через стенки цилиндров компрессора в окружающую среду, а также в промежуточном и конечном холодильнике (при охлаждении газа в них до температуры Т1) определяется как
Q = zQ' + (z – 1) Q'', (9)
где Q' – количество теплоты, отводимое от газа в одной ступени компрессора через стенки цилиндра; Q'' – количество теплоты, отводимое от газа в каждом холодильнике
где T2 – температура газа после сжатия. Газ считается идеальным с постоянной теплоемкостью. Теплоемкости идеального газа определяются по молекулярно-кинетической теории. Удельная изобарная теплоемкость:
Удельная изохорная теплоемкость:
где µ - молярная масса, кг / кмоль. Молярные изобарная mcp и изохорная mcu теплоемкости зависят от числа атомов в молекуле газа и их значения даны в приложении А.2.
Задача 4 на расчет цикла воздушной холодильной машины. Массовый расход воздуха в системе холодильной машины и теоретическая мощность двигателя для привода машины N определяются как
Q0 = mq2 и N = mlц, (14)
где m – массовый расход воздуха; q2 –теплота, отводимая от охлаждаемого объекта одним килограммом воздуха; lц – удельная работа цикла. Теплоемкость воздуха принять не зависящей от температуры и равной cp=1 кДж/(кг∙К), а показатель адиабаты k = cp/cu = 1,4. В задаче 5 определяются основные параметры идеального цикла парокомпрессионной холодильной машины. Поскольку процессы подвода и отвода теплоты в цикле изобарно-изотермические, то удельная (на 1 кг аммиака) теплота, отводимая от охлаждаемого объекта, определяется как q2 = h1 – h4, а теплота, отводимая в окружающую среду q1 = h2 – h3. Так как процесс 3-4 – изоэнтальпийный (h=const), то h4 = h3. Энтропия на выходе из испарителя равна энтропии на выходе из компрессора s1 = s2, поскольку процесс 1-2 изоэнтропный. Энтальпия h1 на выходе из испарителя находится как энтальпия влажного пара при степени сухости, которая, в свою очередь, определяется по известному значению энтропии s1. Задачу решать при помощи таблиц термодинамических свойств аммиака на линиях кипения и конденсации (таблица приложения Б. 1).
|

 и изохорная
и изохорная  теплоемкости в интервале температур от t1 до t2 могут быть определены для каждого из газов смеси по формуле
теплоемкости в интервале температур от t1 до t2 могут быть определены для каждого из газов смеси по формуле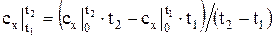 , (1)
, (1)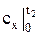 и
и  – средние теплоемкости газов в интервале температур от 0°С до t1 и от 0°С до t2 соответственно, определяемые по таблице приложения А.1.
– средние теплоемкости газов в интервале температур от 0°С до t1 и от 0°С до t2 соответственно, определяемые по таблице приложения А.1. , (2)
, (2) и
и  – средние теплоемкости водорода и диоксида углерода в интервале температур от t1 до t2;
– средние теплоемкости водорода и диоксида углерода в интервале температур от t1 до t2;  и
и  – массовые доли газов.
– массовые доли газов.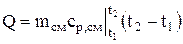 , (3)
, (3) , (4)
, (4) , (5)
, (5) , (6)
, (6) ,
, (7)
(7) , где p1 и pz – давления на входе и выходе многоступенчатого компрессора; z – число ступеней сжатия. При этом теоретическая мощность привода многоступенчатого компрессора определяется как
, где p1 и pz – давления на входе и выходе многоступенчатого компрессора; z – число ступеней сжатия. При этом теоретическая мощность привода многоступенчатого компрессора определяется как , (10)
, (10) , (11)
, (11) , (12)
, (12) (13)
(13)


