Постановка задачи и параметры математической модели. В дальнейшем состав Координационного совета может быть расширен по решению этого органа, исходя из необходимости привлечения к решению стоящих перед ним задач
В дальнейшем состав Координационного совета может быть расширен по решению этого органа, исходя из необходимости привлечения к решению стоящих перед ним задач активных представителей общественных объединений и граждан. Конгресс поручает Координационному совету разработать и принять план работы с учетом наказов участников Конгресса, а также положений декларации «Образование – для всех», итогового документа Московского экономического форума «Экономика для человека», ряда выступлений научных работников РАН на Конференции «Настоящее и будущее науки в России. Место и роль Российской академии наук», предложений по развитию информационного общества от участников Общественного движения «За возрождение отечественной науки». 4. Конгресс считает необходимым приступить к формированию Общественного научного экспертного совета (ОНЭС) для экспертизы принимаемых важных решений, и содействия проведению работ по теме «Стратегия России, обеспечивающая приоритетное развитие человеческого потенциала». Конгресс поручает Координационному совету сформировать ОНЭС из числа авторитетных профессиональных представителей научного, образовательного, инженерного сообществ, работников культуры на принципах ротируемости его членов, публичности работы и персональной ответственности. Мы обращаемся к руководству РАН с предложением оказать содействие созданию и деятельности этого Совета и поддержать проведение работ по теме «Стратегия России, обеспечивающая приоритетное развитие человеческого потенциала». 5. Конгресс считает необходимым инициировать обсуждение вопроса о проведении общероссийского референдума об отмене федерального закона №83-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации в связи с совершенствованием правового положения государственных (муниципальных) учреждений», о пересмотре концепций федеральных законов №253-ФЗ о «реформировании» Российской академии наук, №273-ФЗ «Об образовании в Российской Федерации», а также отмене соответствующих подзаконных актов, в частности, так называемой дорожной карты изменений в сфере образования от 30.12.2012г. Конгресс поручает Координационному совету включить в план работы подготовку соответствующих мероприятий.
Круглые пластины. Моментная теория Постановка задачи и параметры математической модели Задачу удобно решать в цилиндрических координатах, направив ось z по нормали к срединной поверхности, ось r –по радиусу, поместив начало координат в центре пластины. Перемещение по нормали к срединной поверхности –w(r), Гипотеза Бернулли здесь формулируется так: нормаль к срединной поверхности остается прямой. Угол поворота нормали в радиальной плоскости – θ(r). Нагрузка симметрична относительно оси пластины – qz(r)=p(r). Напряжения по нормали к срединной поверхности Примеры – плоское днище цилиндрического сосуда или резервуара, толстая мембрана, цилиндрические упругие элементы, клапана. Параметры задачи: - w(r), перемещение срединной поверхности по оси z; - θ(r), угол поворота нормали в радиальной плоскости; - - Q(r), поперечная сила в радиальной плоскости на единицу длины дуги; - - - - - - В перечне отсутствуют касательные напряжения и поперечные силы в тангенциальной плоскости, так как отсутствуют угловые деформации вследствие симметрии задачи. Касательными напряжениями в радиальной плоскости пренебрегаем как малыми в сравнении с нормальными напряжениями (как и в стержнях). Срединную поверхность считаем не растяжимой. Граничные условия обеспечивают свободу перемещений в радиальном направлении. Все необходимые иллюстрации приведены на рисунке.
|

 малы (порядка давления p) и ими можно пренебречь.
малы (порядка давления p) и ими можно пренебречь. , давление на пластину;
, давление на пластину; , изгибающий момент в радиальной плоскости на единицу длины дуги;
, изгибающий момент в радиальной плоскости на единицу длины дуги; , изгибающий момент в тангенциальной плоскости (касательной к окружности радиусом r) на единицу длины дуги;
, изгибающий момент в тангенциальной плоскости (касательной к окружности радиусом r) на единицу длины дуги;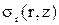 , нормальное напряжение в радиальной плоскости;
, нормальное напряжение в радиальной плоскости; , нормальное напряжение в тангенциальной плоскости;
, нормальное напряжение в тангенциальной плоскости; , линейная деформация в радиальной плоскости;
, линейная деформация в радиальной плоскости; , линейная деформация в тангенциальной плоскости.
, линейная деформация в тангенциальной плоскости.


