Неявное и параметрические задания функций и их дифференцирование. Революция в обработке изображений реального мира произошла с выходом в 1977 году книги Б
Революция в обработке изображений реального мира произошла с выходом в 1977 году книги Б. Мандельброта «Фрактальная геометрия природы». Фрактал - это структура, обладающая схожими формами разных размеров. Такие структуры могут имитироваться с помощью рекурсивных функций. Фракталы не зависят от разрешения устройства. Это масштабированные картинки, которые можно описать небольшим конечным набором инструкций с помощью компьютерной программы. Процесс сжатия изображения состоит из следующих этапов. 1. Разделение изображения на неперекрывающиеся области (домены). Набор доменов должен перекрывать все изображение полностью. 2. Задание набора ранговых областей изображения. Ранговые области могут перекрываться. Они не должны обязательно закрывать всю поверхность картинки. 3. Фрактальное преобразование. Для каждого домена подбирается такая ранговая область, которая после аффинного преобразования наиболее точно аппроксимирует домен. Подобное преобразование не только сжимает и деформирует изображение ранговой области, но и изменяет яркость и контраст. 4. Сжатие и сохранение параметров аффинного преобразования. Файл со сжатым изображением содержит две части: заголовок, включающий в себя информацию о расположении доменов и ранговых областей, и эффективно упакованную таблицу аффинных коэффициентов для каждого домена.
Этапы восстановления изображения такие. 1. Создание двух изображений одинакового размера, А и Б. Их размер может быть не равен размеру исходного изображения. Начальный рисунок областей А и Б не имеет значения. Это могут быть случайные данные, белое или черное. 2. Преобразование данных из области А в область Б. Для этого сначала изображение Б делится на домены так же, как и на первой стадии процесса сжатия (расположение доменов описано в заголовке файла). Теперь для каждого домена области Б проводится соответствующее аффинное преобразование ранговых областей изображения А, описанное коэффициентами из сжатого файла, и результат помещается в область Б. На этой стадии создается совершенно новое изображение. 3. Преобразование данных из области Б в область А. Этот шаг идентичен предыдущему, только изображения Б и А поменялись местами, то есть теперь разделяется на блоки область А и на эти блоки отображаются ранговые области изображения Б. 4. Многократно повторяются второй и третий шаги процедуры восстановления данных до тех пор, пока изображения А и Б не станут неразличимыми. Обманчиво простой процесс попеременного отображения двух изображений друг на друга приводит к созданию репродукции исходной картинки. Точность соответствия зависит от точности аффинного преобразования, коэффициенты которого вычисляются в процессе сжатия. Алгоритмы сжатия и восстановления информации используют целочисленную арифметику и специальные методы уменьшения накапливающихся ошибок округления. В отличие от распространенных в настоящее время методов сжатия/восстановления графических изображений, фрактальное преобразование асимметрично: процесс восстановления нельзя провести путем простой инверсии процедуры сжатия. Сжатие требует гораздо большего количества вычислений, чем восстановление. В процессе фрактального преобразования получается набор цифр, который в очень сжатой форме описывает изображение. Достигаемый при этом большой коэффициент сжатия позволяет хранить и передавать высококачественные изображения. При высоком разрешении исходного изображения фрактальное отображение гораздо более эффективно с точки зрения снижения объема сжатой информации. Глава 4. Тема3. Неявное и параметрические задания функций и их дифференцирование. Пример 3.1. Рассмотрим две функции Имеем Перейдём к точным формулировкам. Определение 3.1. Если функция задана формулой, то говорят, что функция задана явным образом. Пусть Определение 3.2. Если функция является решением некоторого уравнения, то говорят о неявном задании функции. Координаты Пример 3.2. Так уравнение
рис.1 Решение Решение рис.2а рис.2б Таким образом, данное уравнение задаёт нам две различных явно заданных функции. Как конкретизировать функцию при её неявном задании. Очень просто нужна дополнительная информация. Пример 3.3. Уравнение Уравнение При неявном задании функции нужно заранее определить какая из двух переменных Например, если считать в уравнении
Графики данных функций изображены на рис.3.
рис.3а. рис.3б.
Если к уравнению получим только одно явное выражение для функции:
|

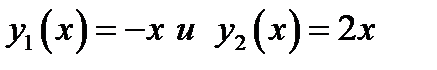 . Эти же две функции можно задать одним алгебраическим уравнением, а именно
. Эти же две функции можно задать одним алгебраическим уравнением, а именно 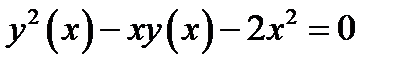 . (3.1) Действительно. Решим это квадратное уравнение относительно неизвестной
. (3.1) Действительно. Решим это квадратное уравнение относительно неизвестной 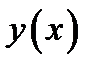 .
.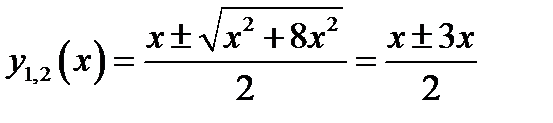 . Откуда получаем
. Откуда получаем 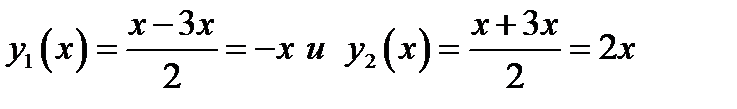 .
.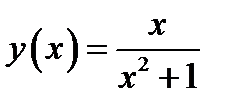 . Значение такой функции легко вычислить. Нужно заданное значение аргумента подставить в формулу и сосчитать полученное выражение. Например
. Значение такой функции легко вычислить. Нужно заданное значение аргумента подставить в формулу и сосчитать полученное выражение. Например 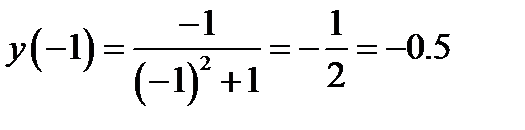 .
.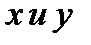 считаются равноправными. Это означает, что можно считать одну из этих переменных функцией, а другую аргументом. Вся сложность при неявном задании функции заключается в вычислении значения функции при заданном значении её аргумента.
считаются равноправными. Это означает, что можно считать одну из этих переменных функцией, а другую аргументом. Вся сложность при неявном задании функции заключается в вычислении значения функции при заданном значении её аргумента.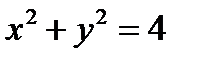 определяет функцию
определяет функцию  . Решая это уравнение относительно
. Решая это уравнение относительно  , получаем
, получаем 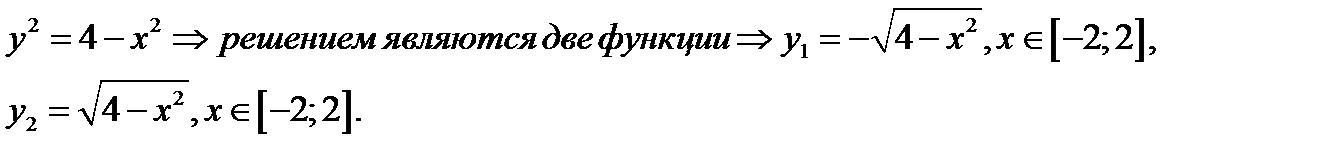
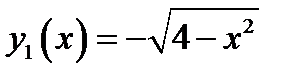 задает нам функцию, график которой приведен на рис.2а.
задает нам функцию, график которой приведен на рис.2а.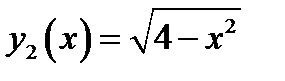 задает нам функцию, график которой приведен на рис.2б.
задает нам функцию, график которой приведен на рис.2б. 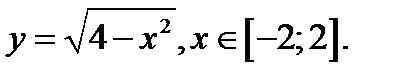
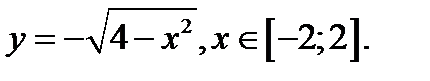
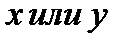 является аргументом, а какая функцией.
является аргументом, а какая функцией.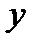 аргументом, а переменную
аргументом, а переменную 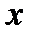 функцией, то уравнение задаёт две функции
функцией, то уравнение задаёт две функции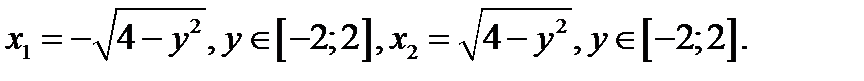

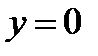 значение
значение 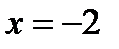 », то
», то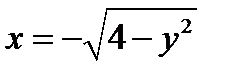 (см. рис.3а).
(см. рис.3а).


