Из формулы (3.4) видно, что при неявном дифференцировании вторая производная зависит от аргумента , от функции и её производной .
Пример 3.5. Найти уравнение касательной и нормальной прямой в точке А Решение. Проверкой убеждаемся, что точка А(1;2) принадлежит линии, задаваемой уравнением. Пусть переменная
и
соответственно. Как видно из этих уравнений нам потребуется значение производной функции в точке касания. Применяя правило неявного дифференцирования, вычисляем производную в точке
Отсюда выписываем уравнение для определения производной и вычисляем Подставляя вычисленные значения в уравнение касательной (5.4), получаем
получаем Параметрические уравнения задания линий. Существует ещё один способ задания линий, при котором координаты считаются равноправными: это задание кривых параметрическими уравнениями. Координаты
Параметр Пример 3.6. Определить уравнения кривых в декартовой системе координат
Решение. Анализируем первую систему уравнений. Возводим оба уравнения системы 1) в квадрат и, складывая, получаем Если при параметрическом задании функции считать переменную Теорема 3.1. Пусть функция Тогда её производная по аргументу
Доказательство. По условию функция разделив обе части на Обозначим для простоты записи в виде Поскольку вторая производная есть производная от первой производной, то применяя правило параметрического дифференцирования к параметрической записи первой производной (3.8) или (что тоже самое 3.9) получаем параметрическую запись второй производной
Контрольные вопросы. I. Как задаётся неявная функция? II. Является ли линия задаваемой неявной функцией графиком? III. Сформулируйте правило дифференцирования неявно заданной функции. От чего зависит полученная производная. IV. Является ли линия, задаваемая параметрическими уравнениями графиком? V. Сформулируйте правило параметрического дифференцирования. Далее предлагаются упражнения по данной теме для самостоятельной работы. В разделе ответы и решения приведены решения упражнений и ответы. Упражнение 3.1 Функция Упражнение 3.2. Доказать, что данные формулы задают одну и туже линию
Упражнение 3.3. Функция и условием (см. пример 3.2) 1) Применяя правило неявного дифференцирования 2) Используя решение примера 3.1. 3) Результаты сравнить. Упражнение 3. 4 Применяя правило неявного дифференцирования, вычислить производные от функций Упражнение 3.5. Применяя правило неявного дифференцирования, вычислить вторую производную от функций
Упражнение 3.6. Вычислить и записать в параметрическом виде первую и вторую производные виде Упражнение 3.7. Вычислить и записать в параметрическом виде первую производную Упражнение 3.8. Написать уравнение касательной и нормали к заданным кривым (см. формулы (3.5),(3.6)). 1)
|

 к линии заданной уравнением
к линии заданной уравнением  .
. будет аргументом функции
будет аргументом функции  . В данном случае функция
. В данном случае функция  задана неявным образом. Уравнения касательной и нормали в точке касания
задана неявным образом. Уравнения касательной и нормали в точке касания 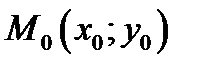 имеют вид
имеют вид (3.5)
(3.5) (3.6)
(3.6)


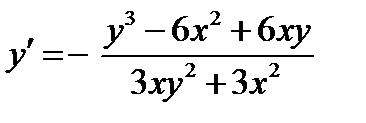 . Поэтому
. Поэтому 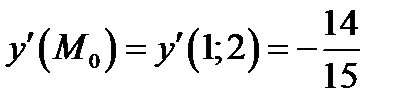
 . Запишем это уравнение в общем виде
. Запишем это уравнение в общем виде 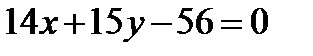 . Подставляя вычисленные значения в уравнение нормали (4.5),
. Подставляя вычисленные значения в уравнение нормали (4.5),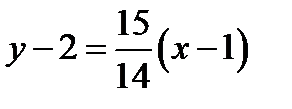 . Или аналогично предыдущему
. Или аналогично предыдущему  .
.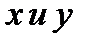
 (скажем, времени)
(скажем, времени) (3.7)
(3.7) .
.
 . Данная кривая это окружность единичного радиуса:
. Данная кривая это окружность единичного радиуса:  . Аналогично для системы 2) получаем
. Аналогично для системы 2) получаем 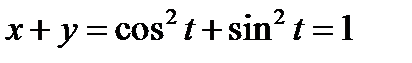 . Это уравнение прямой линии
. Это уравнение прямой линии  .
. функцией, а переменную
функцией, а переменную  аргументом то возникает вопрос каким образом вычислить производную функции
аргументом то возникает вопрос каким образом вычислить производную функции  задана в параметрическом виде
задана в параметрическом виде 
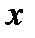
 записывается в параметрическом виде формулами
записывается в параметрическом виде формулами (3.8)
(3.8)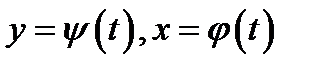 . Откуда
. Откуда  . Дифференцируя обе части по параметру
. Дифференцируя обе части по параметру  и используя цепное правило, получаем
и используя цепное правило, получаем  или
или будем иметь
будем иметь  . Формула (3.8) доказана.
. Формула (3.8) доказана. , тогда формулу (3.8) можно переписать
, тогда формулу (3.8) можно переписать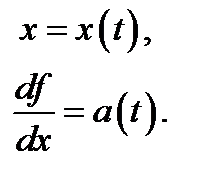 (3.9)
(3.9) (3.10)
(3.10) задана неявно уравнением
задана неявно уравнением 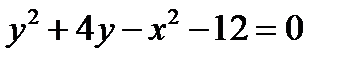 и дополнительным условием: 1)
и дополнительным условием: 1)  ; 2)
; 2) 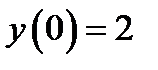 . Найти явную формулу для функции.
. Найти явную формулу для функции.
 определена уравнением
определена уравнением 
 . Вычислить производную
. Вычислить производную 
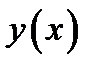 заданных неявно (уравнениями)
заданных неявно (уравнениями) 
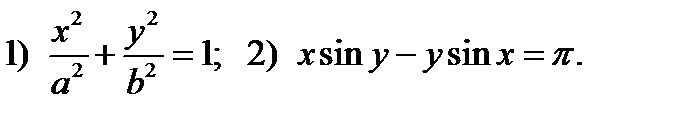
 от функции
от функции  заданной в параметрическом
заданной в параметрическом
 от функций
от функций  4)
4) 
 при
при  ; 2)
; 2) 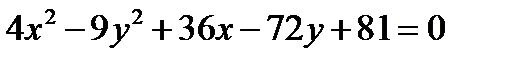 , в точке (0;1).
, в точке (0;1).


