Расчет магнитной цепи синхронной машины при холостом ходе
Расчет магнитной цепи синхронной машины при холостом ходе Расчет магнитной цепи выполняется с целью определения МДС обмотки возбуждения, необходимой для создания требуемого магнитного потока при холостом ходе:
Рис.5.5 где кф - коэффициент формы поля. Магнитная цепь машины на пару полюсов представлена на рис. 5.5. Для расчета магнитной цепи используют уравнение полного тока
Интегрирование ведется вдоль средней силовой линии, разделенной на пять участков: воздушный зазор (1), зубцовая зона статора (2), ярмо статора (3), полюс (4) и ярмо ротора (5) в предположении, что напряженность магнитного поля каждого участка постоянна:
Каждый линейный интеграл определяет магнитное напряжение на соответствующем участке, а сумма токов в левой части представляет собой полный ток обмотки возбуждения, охватываемый контуром интегрирования,
Магнитное напряжение воздушного зазора
bpmi =αδτ - расчетная ширина полюсного наконечника; αδ - коэффициент полюсного го рекрытия; kδ - коэффициент воздушного зазора, учитывающий влияние зубчатости статор и ротора на магнитное сопротивление зазора. Магнитное напряжение зубцов статора
определяется по средней напряженности поля в зубце, равной ее значению на высоте -1/3hz1 от головки зубца. Принимая допущение, что магнитный поток зубцового деления
полностью проходит через зубец, находим индукцию Вz1/3.. на высоте hz1/3.,. от головки зубца:
где ℓm1 - длина сердечника статора; кс = 0,93-0,95 - коэффициент заполнения сердечника сталью; bz1/3 - ширина зубца в сечении на высоте 1/3hz1, от головки зубца. Напряженность поля в зубце Нz1/3 определяется по характеристике намагничивания стали Н= f (В) для найденной индукции Вz1/3. Магнитное напряжение ярма статора
находим по макчимальной напряженности поля в ярме, соответствующей по кривой намагничивания стали Н= f(B) индукции
где hа1 - высота ярма статора. Коэффициент ξ непостоянство напряженности поля На1 по длине участка ℓа1. Магнитное напряжения сердечника полюса определяется по максимальной напряженности поля Нm у основания полюса:
Расчет магнитного поля в полюсе выполняется с учетом потока рассеяния обмотки возбуждения
где σ f = 1,3 -1,4 - коэффициент рассеяния полюсов. Этому потоку соответствует индукция у основания полюса:
где ℓm - расчетная длина сердечника полюса; bm - ширина сердечника полюса. Напряженность поля Нm определяется по кривой намагничивания стали полюса H= f (В) для магнитной индукции Вm. Магнитное напряжение ярма ротора
где Нα2 - максимальная напряженность поля в ярме, соответствующая индукции
Где Lα2 - длина средней силовой линии на участке ярма ротора; ℓα2 - длина ярма ротора; hα2 - высота ярма ротора. Расчет магнитной цели выполняется для 5-7 значений ЭДС E0 в диапазоне от 0,5 до 1,3 UH. Результаты расчетов представляются в виде характеристики холостого хода Е0 = f (F f) или характеристики намагничивания Ф fm = f (F f), построенных в относительных единицах (рис. 5.6). При этом за базисные значения принимаются номинальное напряжение UH, соответствующий ему магнитный поток и МДС возбуждения F f0 при E0 = Uн.
Рис.5.6 Характеристика холостого хода и характеристика намагничивания в относительных единицах совпадают. По характеристике холостого хода определяют коэффициент насыщения
В хорошо спроектированной машине кμ =1,1 – 1,2. При малом насыщении (кμ < 1,1) возрастает масса стали, а при глубоком насыщении (кμ > 1,2) существенно увеличивается ток возбуждения. При нагрузке синхронной машины ток статора создает свое магнитное поле. Большая часть этого поля замыкается через ротор и, взаимодействуя с магнитным полем возбуждения, определяет все основные свойства и характеристики синхронной машины. Процесс такого взаимодействия называется реакцией якоря. А поле статора, участвующее в этом взаимодействии, называют полем реакции якоря. Рассмотрим поле реакции якоря при симметричной нагрузке синхронной машины. Пусть машина работает в генераторном режиме. Обмотку статора изобразим в виде зубцового слоя с плотно уложенными проводниками (рис. 5.7). Фазы обмотки представим их магнитными осями.
Рис.5.7 Ротор вращается с частотой n =60 f 1/p против часовой стрелки. Принимая допущение о том, что МДС обмотки возбуждения F f и созданный ею магнитный поток Ф f являются синусоидальными пространственными волнами, изобразим их в виде вращающихся векторов на комплексной плоскости. Совместим вещественную ось комплексной плоскости с осью фазы А, тогда, согласно рис. 5.7, векторы F f и Ф f можно записать в виде
где F f и Ф f - действующие значения первых гармоник МДС и потока возбуждения. При вращении ротора поток Ф f индуцирует в обмотке статора ЭДС E0, изображающий вектор которой
Согласно этому выражению вектор ЭДС E0 отстает от вектора потока Ф f на 90°. Под действием ЭДС E0 по обмотке статора потечет ток I1, сдвинутый относительно ЭДС E0 на угол ψ1,
Проекции этого тока на фазные оси ABC дают мгновенные значения токов в фазах статора
Как было показано в главе 3, симметричная система трехфазных токов образует результирующую МДС, первая пространственная гармоника которой представляет собой бегущую волну,
Положение максимума этой волны определяется пространственным углом α = ωt - ψ, соответствующим на комплексной плоскости положению изображающего вектора тока I1. Следовательно, синусоидальную пространственную волну результирующей МДС обмотки статора можно представить на комплексной плоскости изображающим вектором, совпадающим по фазе с вектором тока I1,
Система изображающих векторов позволяет наглядно проиллюстрировать характер взаимодействия поля реакции якоря с полем возбуждения. На рис. 5.8 представлены векторные диаграммы при различном характере нагрузки.
Рис.5.8 Если ток статора I1 совпадает по фазе с ЭДС Eo, то вектор МДС реакции якоря F1 отстает от МДС обмотки возбуждения на угол 90°. Такую реакцию якоря при активной нагрузке называют поперечной реакцией якоря. Если ток I1 отстает от ЭДС Eo на угол ψ1 (активно-индуктивная нагрузка), то МДС реакции якоря F1 будет отставать от МДС обмотки возбуждения F f на угол 90°+ψ1. При этом говорят, что реакция якоря носит размагничивающий характер, так как проекция вектора F1 на ось d направлена навстречу вектору F f. Если ток I1 опережает ЭДС Ёo на угол ψ (активно-емкостная нагрузка), то вектор F1 будет отставать от вектора F f на угол 90o – ψ1. В этом случае реакция якоря носит намагничивающий характер, так как проекция F1 на ось d направлена согласно с вектором F f Приведенный анализ дает качественную картину процесса взаимодействия поля реакции якоря с полем возбуждения. Для количественной оценки результатов такого взаимодействия необходимо знать закон распределения магнитного поля реакции якоря в воздушном зазоре. В неявнополюсной машине определение закона распределения магнитного поля реакции якоря не представляет затруднений. Поскольку зазор неявнополюсной машины практически не меняется, то кривая распределения магнитного поля реакции якоря повторяет кривую распределения МДС F1рез независимо от того, какое положение занимает волна МДС относительно ротора. В этом случае магнитную индукцию поля реакции якоря, как и МДС, можно представить на комплексной плоскости в виде вращающегося вектора:
Рис.5.9 В явнополюсных машинах воздушный зазор неравномерный, поэтому характер распределения поля реакции якоря будет зависеть от положения оси поля относительно ротора (то есть от угла ψ1). Это обстоятельство существенно затрудняет расчет поля реакции якоря. Для упрощения расчета применяют принцип наложения, в соответствии с которым поле реакции якоря определяется как сумма двух полей от составляющих МДС F1 по осям симметрии ротора d и q (рис.5.9),
Удобство разложения исходного вектора МДС F1 на составляющие по осям d и q состоит в том, что для определения результирующего поля достаточно построить всего две картины поля: поле реакции якоря по продольной оси (ψ1 = ±90°) и поле реакции якоря по поперечной оси (ψ2 = 0). Кривые распределения магнитных индукций этих полей при синусоидальном распределении МДС представлены на рис. 5.10. Такой метод расчета магнитного поля реакции якоря явнополюсной машины получил название метода двух реакции. Распределение магнитных индукций поля реакции якоря по осям d (рис. 5.10, а) и q (рис.5.10б) имеет существенно несинусоидальный характер, но форма кривых не зависит от характера нагрузки синхронной машины, так как положение полей Bad и Baq относительно ротора остается неизменным.
Рис.5.10 Амплитуды первых гармонях пола реакции якоря получают, разлагая действительную кривую поля в ряд Фурье:
где kd, kq - коэффициенты формы поля продольной и поперечной реакции якоря. Коэффициенты kd и кq так же, как и коэффициент формы поля обмотки возбуждения k f явнополюсной машины, зависят от геометрических размеров магнитной цепа на участке воздушного зазора:
Эти зависимости могут быть получены на основе расчета магнитного поля реакции якоря. Они приводятся в руководствах по проектированию синхронных машин. Для количественной оценки влияния поля реакции якоря на результирующее поле машины необходимо выполнить сложение первых гармоник индукций поля возбуждения B f1 и поля статора Ba1.:
С другой стороны, результирующее поле В(1. можно связать с суммарной МДС Fμ1
полагая, что она создается обмоткой, эквивалентной обмотке возбуждения. Для расчета МДС Fμ1 уравнение магнитных индукций (5.5) преобразуете» в уравнение МДС. В случае неявнополюсной машины имеем
отсюда, разделив вес члены этого уравнения на
ка - коэффициент реакции якоря. Аналогичные преобразования выполняются и для машины с явновыраженными полюсами:
Отсюда получаем уравнение МДС:
возбуждения; kad -коэффициент реакции якоря по поперечной оси. Приведение МДС обмотки статора к обмотке возбуждения позволяет вместо сложения магнитных полей складывать непосредственно МДС реакции якоря и обмотки возбуждения с учетом их пространственной ориентировки по отношению друг к другу. При этом отпадает необходимость в раздельном определении магнитных полей. Результирующее поле определяется по суммарной МДС Fμ1, что особенно важно в случае насыщенной магнитной цепи, когда принцип наложения магнитных полей несправедлив.
|

 (5.1)
(5.1)
 (5.2)
(5.2) (5.3)
(5.3) (5.4)
(5.4)
 - максимальная индукция в зазоре; ℓδ - расчетная длина машины;
- максимальная индукция в зазоре; ℓδ - расчетная длина машины;

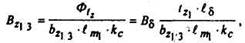













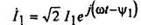


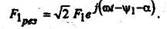








 (5.5)
(5.5)

 получаем
получаем
 - МДС обмотки статоре, приведенная к обмотке возбуждения;
- МДС обмотки статоре, приведенная к обмотке возбуждения;

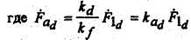 МДС продольной реакции якоря, приведенная к МДС обмотки возбуждения; каd - коэффициент реакции якоря по продольной оси;
МДС продольной реакции якоря, приведенная к МДС обмотки возбуждения; каd - коэффициент реакции якоря по продольной оси; -МДС поперечной реакции якоря, приведенная к МДС обмотки
-МДС поперечной реакции якоря, приведенная к МДС обмотки


