Неявнополюсный генератор. В насыщенной машине исключается возможность раздельного определения потоков от МДС возбуждения Ff и МДС реакции якоря Fa
В насыщенной машине исключается возможность раздельного определения потоков от МДС возбуждения F f и МДС реакции якоря Fa. В этом случае результирующий поток Фμ определяется по суммарной МДС
Если пренебречь потоками рассеяния Фσ f . и Фσ, то можно считать, что насыщение генератора при нагрузке определяется только результирующим потоком Фμ. В неявнополюсном генераторе магнитное сопротивление для этого потока не зависит от положения его оси относительно ротора, поэтому суммарная МДС Fμ при нагрузке создает такой же магнитный поток, что и равная ей МДС обмотки возбуждения F f в режиме холостого хода. Отсюда следует, что связь между Фμ и Fμ будет определяться кривой намагничивания генератора при холостом ходе (рис. 5.16). В относительных единицах эта кривая совпадает с характеристикой холостого хода (х.х.х.), поэтому по ней можно определить ЭДС Еμ, соответствующую суммарной МДС Fμ Рис.5.16 В действительности на насыщение стали заметное влияние оказывают потоки рассеяния обмоток статора и возбуждения. При изменении нагрузки соотношение между потоками рассеяния и результирующим потоком меняется, поэтому кривая намагничивания при нагрузке будет также меняться, отклоняясь от характеристики холостого хода (пунктирная линия на рис. 5.16). Величина ЭДС Еμ, найденная по этой кривой совместно с ЭДС рассеяния Еσ, определяет напряжение насыщенного генератора:
Расчет магнитной характеристики генератора при нагрузке весьма сложен, поэтому часто пользуются характеристикой холостого хода, заменяя Еμ на Еμr и внося поправку в величину сопротивления рассеяния обмотки статора:
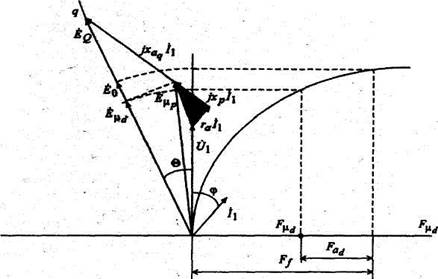
где xр > ха - сопротивление Потье, названное по имени автора, предложившего этот метод. Сопротивление Потье должно быть такой величины, чтобы расчетной ЭДС Eμp по характеристике холостого хода соответствовало действительное значение суммарной МДС Fμ. Уравнения МДС (5.11), напряжений (5.12) и характеристика холостого хода (рис. 5.16) позволяют рассчитать рабочие режимы синхронного генератора с учетом насыщения. Пусть требуется рассчитать МДС обмотки возбуждения F f, обеспечивающую требуемое напряжение U1 при нагрузке, заданной током I1 и коэффициентом мощности cosφ. Решение выполняется графическим методом с помощью векторной диаграммы (рис. 5.17). На оси ординат характеристики холостого хода откладывается вектор напряжения U1.
Рис.5.17
Модуль этой ЭДС определяет по характеристике холостого хода суммарную МДС Fμ,. Вектор Fμ опережает вектор ЭДС Еμr на 90". Вычитая из него (согласно (5.11)) вектор МДС реакции якоря Fa находим искомый вектор МДС обмотки возбуждения:
Обращаясь вновь к характеристике холостого хода, определяем по модулю МДС F f величину ЭДС холостого хода Eo. Вектор ЭДС Eo отстает от вектора МДС обмотки возбуждения F f на 90°. Угол между векторами Eo и U1 определяет рабочий угол Θ, а разница модулей этих векторов ΔU=Eo-U1 показывает величину изменения напряжения генератора при сбросе нагрузки. По условиям безопасности работы генератора и вспомогательного оборудования, получающего питание от генератора, величина ΔU не должна превышать 40% UH. Суммарная МДС насыщенного генератора
определяет результирующий поток
который наводит в обмотке статора ЭДС
Магнитная характеристика яваополюсного генератора Фμ = f (Fμ)имеет очень сложный характер из-за неравномерности воздушного зазора. С целью упрощения расчетов разделим результирующий поток Фμ на продольную Фμd и поперечную Фμq составляющие,
и примем допущение, что магнитная цепь по поперечной оси не насыщена. Насыщение будем учитывать лишь по продольной оси, используя магнитную характеристику холостого хода
Составляющие результирующего потока Фμd. и Фμq наводят в обмотке статора ЭДС Eμd и Еμq. Сумма этих ЭДС
совместно с ЭДС рассеяния Еσ = -jxσI1 определяет напряжение генератора
Так как магнитная цепь по поперечной оси принимаете! ненасыщенной, то для расчета ЭДС Eμq можно воспользоваться ранее полученным выражением
а расчет МДС Eμd, как и в случае неявнополюсной машины, выполняется по характеристике холостого хода
Для снижения погрешностей расчета, обусловленных принятыми допущениями, сопротивление рассеяния ха заменяется на сопротивление Потье хр. Рассмотрим задачу определения МДС обмотки возбуждения F f явнополюсного генератора, необходимую для получения напряжения U1 при нагрузке, заданной током I1 и коэффициентом мощности cosφ. Решение выполняется графическим методом с использованием характеристики холостого хода и векторной диаграммы. На оси ординат характеристики холостого хода откладывается вектор U1, а вектор тока I1 направляется под углом φ (рис. 5.18). Зная положение этих векторов, находим ЭДС от результирующего поля
и эквивалентную ЭДС ненасыщенного генератора
которая, как было показано ранее, действует по поперечной оси машины. Поэтому проекция вектора Eμp на эту ось определяет вектор ЭДС Eμd,. Обращаясь к характеристике холостого хода, находим по модулю ЭДС Eμd суммарную МДС генератора по продольной оси Fμd, Эта МДС с учетом реакции якоря по продольной оси Fad. определяет МДС обмотки возбуждения
Рис.5.18 Этой МДС по характеристике холостого ходе соответствует ЭДС Eо. Вектор ЭДС Eо направлен по поперечной оси.
|

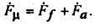

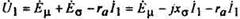

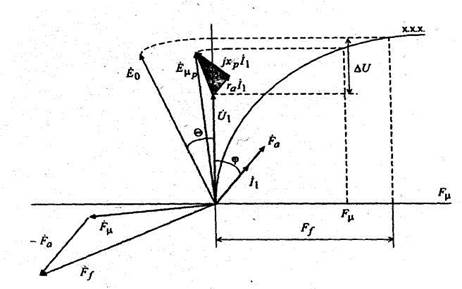
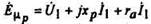





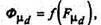
 суммарная МДС генератора по продольной оси.
суммарная МДС генератора по продольной оси.