Сравнивая (5.7) с (5.2), приходим к выводу, что напряжённость электрического поля заряженного шара равна напряжённости такого же точечного заряда, расположенного в центре шара.
1. Карпман В.Л., Белоцерковский З.Б., Гудков И.А. Тестирование в спортивной медицине. - М.: ФиС, 1988. – 208 с. 2. Кондратьев В. В., Антонович А.А. Историческое фехтование. М.: ФАИР-Пресс, 2000. - 208 с. 3. Положение о проведении чемпионата России по историческому фехтованию. М.: ОИФ при ФФ России, 2000. – 8 с. 4. Попов Г.И., Резинкин В.В., Акопян А.О. Сопряженная техническая и физическая подготовка в спортивных единоборствах. // Теория и практика физической культуры. - 2000 - номер 7. - С. 42-45 5. Акопян А.О., Арансон М.В. Специализированная скоростно-силовая подготовка в историческом фехтовании. // Материалы XIII научно-практической конференции «Человек, здоровье, физическая культура и спорт в изменяющемся мире». Коломна, 2003. – С. 144-145. 6. Столяр С. Специальная физическая подготовка юных спортсменов в видах единоборств с учетом требований соревновательной деятельности: Дис.... к.п.н. - М.: ВНИИФК, 1995. - 117 с.
Отсюда напряжённость электрического поля на расстоянии r от центра заряженной сферы равна
Сравнивая (5.7) с (5.2), приходим к выводу, что напряжённость электрического поля заряженного шара равна напряжённости такого же точечного заряда, расположенного в центре шара. 13. Напряженность электростатического поля шара. Равномерно заряженного по объему. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ = dQ/dV – заряд, который приходится на единицу объема). Учитывая соображения симметрии, аналогичные п.3, можно доказать, что для напряженности поля вне шара получится тот же результат, что и в случае (3). Внутри же шара напряженность поля будет иная. Сфера радиуса r'<R охватывает заряд Q'=(4/3)πr'3ρ. Поэтому, используя теорему Гаусса, 4πr'2E=Q'/ε0=(4/3)πr'3ρ/ε0. Т.к. ρ=Q/(4/3πR3)) получаем
Значит, напряженность поля вне равномерно заряженного шара описывается формулой (3), а внутри его изменяется линейно с расстоянием r' согласно зависимости (4). График зависимости Е от r для рассмотренного случая показан на рис. 5. 14. Работа сил электростатического поля по перемещению заряда. Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда
где
где
Пусть заряд
Как видно из рисунка
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно
15. Теорема о циркуляции вектора напряженности электростатического поля. Существуют два равнозначных определения консервативной силы. Оба они подробно обсуждались в механике. Консервативной называется сила, работа которой не зависит от формы траектории. Консервативной называется сила, работа которой на замкнутой траектории равна нулю. Рассмотрим перемещение заряда q в электростатическом поле . Работа этой силы на замкнутой траектории L = L1 + L2 равна нулю: . Это уравнение, упростив, запишем так:
Разберём подробно последнее уравнение. Подынтегральное выражение — элементарная работа электрической силы, действующей на единичный положительный заряд, на перемещении здесь q = 1 — единичный заряд. При подсчёте работы на замкнутой траектории необходимо сложить элементарные работы электрической силы на всех участках траектории. Иными словами, проинтегрировать (3.19) по замкнутому контуру L:
. Интеграл по замкнутому контуру Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю:
Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю. Интеграл 16. Потенциал и разность потенциалов электростатического поля. Эквипотенциальные поверхности. Потенциал электростатического поля — отношение потенциальной энергии заряда в поле к этому заряду:
Выражается потенциал в вольтах: Потенциал j не зависит от заряда q, помещенного в данную точку поля. Для однородного поля потенциал зависит от напряженности E и от расстояния d от данной точки поля до нулевого потенциального уровня.
рис. 2 Работа поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность характеризует потенциал в данной точке поля созданного точечным зарядом Q смотри рис. 2.
где Q — заряд создающий поле, R — расстояние от данной точки поля до заряда Q. Потенциальная энергия электрического взаимодействия системы n точечных зарядов qi равна Wп = 1/2åqij i (1.14) здесь j i — потенциал поля в точке, где находится заряд qi Если поле создано двумя зарядами, то выполняется следствие принципа суперпозиции полей. j = j 1 + j 2 Потенциал поля, созданного несколькими заряженными телами, равен алгебраической сумме потенциалов отдельных полей, создаваемых в данной точке пространства каждым из заряженных тел:
|


 4)
4) из одной точки электростатического поля в другую на отрезке пути
из одной точки электростатического поля в другую на отрезке пути  , по определению равна
, по определению равна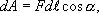
 - угол между вектором силы F и направлением движения
- угол между вектором силы F и направлением движения  из точки “а” в точку “b” будет равна
из точки “а” в точку “b” будет равна
 - кулоновская сила, действующая на пробный заряд
- кулоновская сила, действующая на пробный заряд 
 перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии
перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии  в точку “b”, удаленную от q на расстоянии
в точку “b”, удаленную от q на расстоянии 

 тогда получим
тогда получим

 по замкнутой траектории/ Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:
по замкнутой траектории/ Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:

 . (3.18)
. (3.18)
 (3.20)
(3.20) =
=  называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.
называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.
 - называется циркуляцией вектора напряженности. Т.о. теорема о циркуляции: циркуляция вектора напряженности электростатического поля равна нулю. Из теоремы о циркуляции следует, что силовые линии не могут быть замкнутыми: они начинаются и кончаются на зарядах или уходят в бесконечность. Физический смысл теоремы о циркуляции заключается в том, что электрическое поле - потенциально.
- называется циркуляцией вектора напряженности. Т.о. теорема о циркуляции: циркуляция вектора напряженности электростатического поля равна нулю. Из теоремы о циркуляции следует, что силовые линии не могут быть замкнутыми: они начинаются и кончаются на зарядах или уходят в бесконечность. Физический смысл теоремы о циркуляции заключается в том, что электрическое поле - потенциально.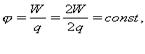 (1.9)
(1.9)
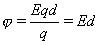

 (1.10),
(1.10),


