Средние пропорциональные отрезки в прямоугольном треугольнике.
Введем понятие среднего пропорционального двух положительных чисел: Средним пропорциональным (средним геометрическим) двух положительных чисел a и b называется число
· Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное проекций катетов на гипотенузу. · Катет прямоугольного треугольника есть среднее пропорциональное гипотенузы и проекции этого катета на гипотенузу. Дано: Δ ABC; Ð A = 90°;
Доказать:
Доказательство: 1. По теореме о сумме углов треугольников Ð B = 90° ‑ Ð BAD = Ð CAD. 2. Δ ABD ~ Δ CAD по двум углам (Ð B = Ð CAD, Ð ADB = Ð CDA = 90°); Þ по определению подобных треугольников, 3. Δ ABD ~ Δ CBA по двум углам (Ð B – общий, Ð ADB = Ð CAB = 90°); Þ по определению подобных треугольников, Следствие: Проекции катетов прямоугольного треугольника на гипотенузу пропорциональны квадратам соответствующих катетов (рисунок 11). Дано: Δ ABC; Ð A = 90°;
Доказать: Доказательство: По теореме о средних пропорциональных отрезках в прямоугольном треугольнике, Итак, в прямоугольном треугольнике выполняются следующие соотношения (рисунок 11):
|

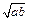 . Название «среднее пропорциональное» связано с тем, что
. Название «среднее пропорциональное» связано с тем, что  , Þ
, Þ  Û
Û 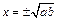 .
. Оказывается, при проведении высоты к гипотенузе прямоугольного треугольника (рисунок 11) образуется 3 подобных треугольника, в результате чего образованные в треугольнике отрезки связаны замечательными соотношениями. Эти соотношения устанавливает теорема о средних пропорциональных отрезках в прямоугольном треугольнике:
Оказывается, при проведении высоты к гипотенузе прямоугольного треугольника (рисунок 11) образуется 3 подобных треугольника, в результате чего образованные в треугольнике отрезки связаны замечательными соотношениями. Эти соотношения устанавливает теорема о средних пропорциональных отрезках в прямоугольном треугольнике: AD – высота.
AD – высота. ;
; .
. ; Þ
; Þ  ; Þ
; Þ 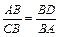 ; Þ
; Þ  ; Þ
; Þ  . #
. # AD – высота.
AD – высота.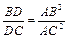 .
.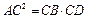 . Тогда
. Тогда  . #
. # ;
; ;
; ;
;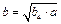 ;
;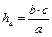 .
.


