Второй признак подобия треугольников. Ключевая задача о высотах треугольника.
Второй признак подобия треугольников (по двум сторонам и углу между ними): Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами, равны, то треугольники подобны (рисунок 8).
Доказать: Δ ABC ~ Δ A 1 B 1 C 1. Доказательство: 1. Построим Δ A 1 B 2 C 1: Ð A 1 C 1 B 2 = Ð C, Ð C 1 A 1 B 2 = Ð A = Ð C 1 A 1 B 1. Тогда Δ ABC ~ Δ A 1 B 2 C 1 по двум углам, Þ по определению подобных треугольников, 2. По условию,
Объединяя эти равенства, получим: 3. Δ A 1 B 2 C 1 = Δ A 1 B 1 C 1 по двум сторонам и углу между ними: A 1 C 1 – общая, A 1 B 1 = A 1 B 2 из пункта 2, Ð C 1 A 1 B 2 = Ð C 1 A 1 B 1 по построению; Þ по определению равных треугольников, Ð A 1 C 1 B 2 = Ð A 1 C 1 B 1. 4. Итак, Ð A = Ð C 1 A 1 B 1 по условию, Ð C = Ð A 1 C 1 B 2 = Ð A 1 C 1 B 1 из доказанного; Þ Δ ABC ~ Δ A 1 B 1 C 1 по двум углам. #
Ключевая задача о высотах треугольника: Если AA 1 и CC 1 – высоты треугольника ABC, то треугольник A 1 BC 1 подобен треугольнику ABC (рисунки 9а и 9б). Дано: Δ ABC;
Доказать: Δ ABC ~ Δ A 1 BC 1. Доказательство: На рисунках 9а и 9б представлены случаи, соответствующие острому и тупому углам B соответственно. Сразу отметим, что если угол B прямой, то основания высот A 1 и C 1 совпадут с вершиной B, и треугольник A 1 BC 1 «превратится» в точку. 1. 2. Δ ABC ~ Δ A 1 BC 1 по двум сторонам и углу между ними (в случае а угол при вершине B – общий, в случае б Ð ABC = Ð A 1 BC 1 как вертикальные; Замечание: Следует обратить внимание на порядок вершин подобных треугольников ABC и A 1 BC 1: если вершины одного из них обходятся по часовой стрелке, то вершины второго – против часовой стрелки. При решении задач второй признак подобия, как правило, используется в сочетании с первым признаком подобно тому, как это было сделано в решении ключевой задачи о высотах. То есть сначала с использованием первого признака доказывается подобие треугольников, из которого делается вывод о пропорциональности сторон; затем, пользуясь полученной пропорциональностью сторон, доказывается подобие другой пары треугольников, опираясь на второй признак.
|

 Дано: Δ ABC, Δ A 1 B 1 C 1;
Дано: Δ ABC, Δ A 1 B 1 C 1; Ð A = Ð A 1;
Ð A = Ð A 1;  .
. .
.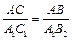 .
. , Þ A 1 B 1 = A 1 B 2.
, Þ A 1 B 1 = A 1 B 2.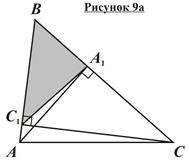 Второй признак подобия треугольников позволяет доказать факт, значительно облегчающий решение некоторых задач, который мы назовем ключевой задачей о высотах треугольника:
Второй признак подобия треугольников позволяет доказать факт, значительно облегчающий решение некоторых задач, который мы назовем ключевой задачей о высотах треугольника: AA 1, CC 1 – высоты Δ ABC.
AA 1, CC 1 – высоты Δ ABC. Δ AA 1 B ~ Δ CC 1 B по двум углам (Ð AA 1 B = Ð CC 1 B = 90°; в случае а угол при вершине B – общий, в случае б Ð ABA 1 = Ð CBC 1 как вертикальные); Þ по определению подобных треугольников
Δ AA 1 B ~ Δ CC 1 B по двум углам (Ð AA 1 B = Ð CC 1 B = 90°; в случае а угол при вершине B – общий, в случае б Ð ABA 1 = Ð CBC 1 как вертикальные); Þ по определению подобных треугольников  Û
Û  .
.


