Определение и свойства подобных треугольников.
Определение и свойства подобных треугольников. Напомним, что числа a1, a2, a3, …, an называются пропорциональными числам b1, b2, b3, …, bn, если выполняется равенство:
Прежде чем дать определение подобных треугольников, рассмотрим два треугольника с попарно равными углами (на рисунке 1 Ð A = Ð A 1, Ð B = Ð B 1, Ð C = Ð C 1). Стороны, противолежащие соответственно равным углам треугольников с попарно равными углами, называются сходственными. Так, на рисунке 1 стороны AB и A 1 B 1, AC и A 1 C 1, BC и B 1 C 1, ‑ сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A 1 B 1 C 1. Дадим теперь определение подобных треугольников:
Замечание 1: Равные треугольники подобны с коэффициентом 1. Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, применительно к изображенным на рисунке 2 треугольникам некорректно говорить, что Δ ABC ~ Δ B 1 C 1 A 1. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что Ð A = Ð K, Ð B = Ð N, Ð C = Ð L, и Замечание 3: Требования, предъявленные определением к подобным треугольникам, являются избыточными. Ниже будут доказаны признаки подобия треугольников, предъявляющие меньше требований к подобным треугольникам. Сформулируем свойства подобных треугольников: 1. Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия (линейными называются величины, измеряемые в единицах длины; к примеру, сторона, периметр, медиана – линейный элемент, а угол или площадь – нет). Примем сформулированное свойство без доказательства, поскольку доказательство для общего случая (для произвольных линейных элементов) использует понятие преобразования подобия, предлагаемого к изучению в IX классе. Следует отметить, что никакие из сформулированных ниже теорем не опираются на данное свойство. 2. Отношение площадей подобных треугольников равно квадрату коэффициента их подобия. Пусть треугольники ABC и A 1 B 1 C 1 подобны с коэффициентом k (рисунок 2). Докажем, что Замечание: В IX классе будет дано определение подобия произвольных фигур. Сформулированные выше свойства подобных треугольников останутся справедливыми и для произвольных фигур.
|

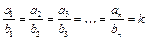 , где k – число, называемое коэффициентом пропорциональности. Например, числа 6, ‑7,5 и 15 пропорциональны числам ‑4, 5 и ‑10 с коэффициентом пропорциональности ‑1,5, поскольку
, где k – число, называемое коэффициентом пропорциональности. Например, числа 6, ‑7,5 и 15 пропорциональны числам ‑4, 5 и ‑10 с коэффициентом пропорциональности ‑1,5, поскольку  .
. Замечание: О пропорциональности чисел имеет смысл говорить, если они связаны пропорцией. А так как пропорцию можно составить не менее чем из четырех чисел, понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка пропорциональна другой, и т.д.).
Замечание: О пропорциональности чисел имеет смысл говорить, если они связаны пропорцией. А так как пропорцию можно составить не менее чем из четырех чисел, понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка пропорциональна другой, и т.д.).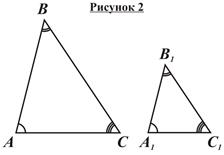 Два треугольника называются подобными, если их углы попарно равны, а сходственные стороны пропорциональны. При этом отношение сходственных сторон подобных треугольников называется коэффициентом подобия. Обозначаются подобные треугольники следующим образом: Δ ABC ~ Δ A 1 B 1 C 1. Итак, на рисунке 2
Два треугольника называются подобными, если их углы попарно равны, а сходственные стороны пропорциональны. При этом отношение сходственных сторон подобных треугольников называется коэффициентом подобия. Обозначаются подобные треугольники следующим образом: Δ ABC ~ Δ A 1 B 1 C 1. Итак, на рисунке 2  где k – коэффициент подобия. Из рисунка 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.
где k – коэффициент подобия. Из рисунка 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом. .
. . Поскольку углы подобных треугольников попарно равны, Ð A = Ð A 1, и по теореме об отношении площадей треугольников, имеющих по равному углу,
. Поскольку углы подобных треугольников попарно равны, Ð A = Ð A 1, и по теореме об отношении площадей треугольников, имеющих по равному углу, 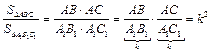 (здесь учтено, что в силу подобия
(здесь учтено, что в силу подобия  ). #
). #


