Свойство медиан треугольника. Ключевая задача о медианах треугольника.

Первый признак подобия треугольников позволяет доказать свойство медиан треугольника:

Свойство медиан треугольника: Медианы треугольника пересекаются в одной точке, называемой центроидом треугольника, и делятся этой точкой в отношении 2:1, считая от вершины (рисунок 6).

Дано:

Δ ABC;

AA ₁, BB ₁, CC ₁ – медианы;

AA ₁Ç CC ₁ = O.

Доказать: BB ₁Ç CC ₁ = O;

.

Доказательство:

1. Проведем среднюю линию A ₁ C ₁. По теореме о средней линии треугольника A ₁ C ₁ïê AC, и .

2. D AOC ~ D A ₁ OC ₁ по двум углам (Ð AOC = Ð A ₁ OC ₁ как вертикальные, Ð OAC = Ð OA ₁ C ₁ как внутр. н/л при A ₁ C ₁ïê AC и секущей AA ₁); Þ по определению подобных треугольников .

3. Пусть BB ₁Ç CC ₁ = O ₁. Аналогично пунктам 1 и 2 можно доказать, что . Но поскольку на отрезке CC ₁ существует единственная точка O,

 

делящая его в отношении CO: OC ₁=2:1, точки O и O ₁ совпадают. А значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2:1, считая от вершины. #

При изучении темы «площади многоугольников» были сформулированы и доказаны три факта о равновеликих треугольниках в фигурах. В частности, было показано, что медиана разбивает произвольный треугольник на две равновеликие части. Оказывается, при пересечении трех медиан треугольника образуется шесть равновеликих треугольников. Назовем этот факт ключевой задачей о медианах треугольника:

Ключевая задача о медианах треугольника: Медианы произвольного треугольника разбивают его на шесть равновеликих треугольников (рисунок 7).

Дано:Δ ABC; AA ₁, BB ₁, CC ₁ – медианы;

AA ₁Ç BB ₁ = BB ₁Ç CC ₁ = O.

Доказать:

.

Доказательство:

1. Обозначим . Тогда поскольку OB ₁ – медиана треугольника AOC, .

2. AH – общая высота треугольников AOB ₁ и AOB, Þ по свойству медиан треугольника, Þ S _{Δ AOB} = 2 S.

3. Т.к. OC ₁ – медиана треугольника AOB, .

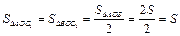4. Аналогично доказывается, что . Итак, . #