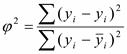Анализ полученных результатов.
Для проверки общего качества уравнения регрессии используются: R - квадрат (коэффициент множественной детерминации). Он характеризует долю вариации (разброса) зависимой переменной (производительности
труда), объясненной с помощью данного уравнения, т. е. обусловленной влиянием на нее отобранных, то есть включенных в модель факторов (процент прибыли и энерговооруженность). Множественный R – коэффициент множественной корреляции, который служит основным показателем тесноты корреляционной связи. Данный коэффициент изменяется от 0 до 1.Если R=1, то связь между Y с одной стороны и аргументами х1, х3 с другой стороны является функциональной и линейной. Если R=0, то отсутствует линейная корреляционная связь, что не исключает, однако наличие в этом случае нелинейной зависимости. Во всех случаях, то есть 0<R<1, считается, что между У и х1, х3 имеется более или менее сильная корреляционная зависимость. Стандартная ошибка - это допустимое отклонение теоретического результирующего фактора от фактического. F-критерий Фишера. Проверяется нулевая гипотеза, смысл которой заключается в том, что все коэффициенты линейной регрессии за исключением свободного члена равны нулю, и, следовательно, фактор хi не оказывает влияния на результат у. Значение F-критерия признается достоверным, если оно больше табличного, тогда нулевая гипотеза отклоняется и уравнение регрессии признается значимым. В данной задаче значимость F близка к нулю, т.е. такова вероятность принятия нулевой гипотезы. t-статистика Стьюдента. Оценивается значимость коэффициентов регрессии. Эта оценка проводится путем проверки гипотезы о равенстве нулю k-го коэффициента регрессии (k = 1,2,..., m). Расчетное значение t-критерия с числом степеней свободы (n-m-1) находят путем деления k-го коэффициента регрессии на среднеквадратическое отклонение этого коэффициента, которое в свою очередь вычисляется как квадратная дисперсия остаточной компоненты и k-го диагонального элемента матрицы, обратной матрице системы нормальных уравнений относительно параметров модели. Это расчетное значение сравнивается с табличным значением критерия Стьюдента при заданном уровне значимости, и если оно больше табличного значения, коэффициент регрессии считается значимым. В противном случае соответствующий данному коэффициенту регрессии фактор следует исключить из модели, при этом качество модели не ухудшится. Р-значение – это вероятность принятия нулевой гипотезы по каждому коэффициенту. Нижние 95% и верхние 95% - это доверительный интервал для нахождения уравнения регрессии (границы нахождения значений коэффициентов регрессии).
III Проверка выполнения условий адекватности модели Существует 4 обязательных свойства, которым должны отвечать «Остатки», чтобы найденное уравнение регрессии было адекватным: • Случайность колебаний уровней остаточной последовательности; • Соответствие распределения случайной компоненты нормальному закону распределения; • Равенство нулю математического ожидания случайной компоненты; • Независимость значений уровней случа йной компоненты.
Рассмотрим способы проверки этих свойств: 1) Для исследования случайности отклонений от уравнения регрессии находят разности ɛi= yi -
Кmax < [3,3lg(n+1)]; ν > [1/2 (n+1-1,96√n-1)],
Где Кmax- общая протяженность самой длинной серии, а ν- общее число серий. В работе вычислены результаты, согласно которым Кmax=2 < 4, а ν= 12> 6. Отсюда следует, что данная модель отвечает первому свойству.
2) Проверка второго свойства производится с помощью нахождения показателей асимметрии γ1 и эксцесса γ2. В качестве оценки асимметрии используются формулы: Если одновременно выполняются условия |
В данной работе
3) Проверка адекватности осуществляется на основе t- критерия Стьюдента по формуле где
4) Проверка независимости значений уровней случа йной компоненты производится на основе d – критерия Дарбина – Уотсона по формуле:
Далее сравниваем полученное значение с критическими верхним d2 и нижним d1 . В работе получено значение d = 2, 25. Это значение больше верхнего табличного d2 , а значит гипотеза о независимости уровней остаточной последовательности принимается. ІV Определение точности модели Точность модели характеризуется величиной отклонения выхода модели от реального значения моделируемой переменной. Для показателя, представленного рядом значений, точность определяется как разность между значениями фактического уровня ряда и его оценкой, полученной расчетным путем с использованием моделей. При этом в качестве статистических показателей точности применяют следующие: 1) Среднее квадратическое отклонение Где i = 1…n;
n- количество наблюдений; p- количество независимых параметров. Значение среднего квадратического отклонения в работе = 6,23 2) Средняя относительная ошибка аппроксимации Результат, полученный в работе =90,74 3) Коэффициент сходимости Результат, полученный в работе = 5,38 4) Коэффициент детерминации Результат, полученный в работе = -4,38
Выводы Множественный R, характеризующий тесноту связи между результирующим показателем и независимыми переменными, равен 0,99 (R приближено к 1) показывает, что связь между Y с одной стороны и аргументами х2, х3 с другой стороны является функциональной и линейной; Значение множественного коэффициента детерминации (R2), равное 0,98 свидетельствует о значительном влиянии включенных в модель факторов на результирующий показатель; Стандартная ошибка - это допустимое отклонение теоретического результирующего фактора от фактического. В рассматриваемом варианте она равна 16,74; Уровень значимости F = 1,003T-15 характеризует среднюю вероятность принятия нулевой гипотезы по уравнению в целом; коэффициенты уравнения регрессии: b1 = 0,66, b3 = 13,03 - показывают среднее изменение результата с изменением факторов на одну единицу, коэффициент а = 31,75. Формально а - значение при х1 и х3 = 0. Если признак фактор Х не имеет и не может иметь нулевого значения, то трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Интерпретировать можно только знак при параметре а. Р-значение - это вероятность принятия нулевой гипотезы по каждому коэффициенту уравнения регрессии. В данном расчетном случае она составляет 0,07 Нижние 95% и верхние 95% - это уровень доверия, которому соответствует 5%-ный уровень значимости, то есть вероятности ошибки. Значения этих показателей определяют минимальный и максимальный уровень коэффициентов, используемых в уравнении при 5%-ном уровне значимости. На основании этих характеристик можно сделать вывод, о том, что модель достаточно точна, адекватна и пригодна для прогнозирования.
Корреляционная связь, описанная уравнением: у = 58,15 + 0,58х2 + 8,18х3
с большой долей вероятности точно характеризует взаимосвязь результирующего показателя (производительности труда) с энерговооруженностью и процентом прибыли.
Заключение В настоящее время множественная регрессия - один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Согласно произведенным расчетам по всем трем таблицам, мы нашли, что уравнение множественной регрессии имеет вид: у = 58,15 + 0,58х2 + 8,18х3
Так же мы провели экономический анализ полученных результатов и убедились в том, что: а) наличие зависимости между Xi и Y является достоверной; б) имеется сильная корреляционная зависимость между Y и Хi; в) коэффициенты регрессии являются значимыми. Таким образом, модель может быть признана адекватной. В целом данное уравнение можно использовать для определения по нему расчетного значения производительности труда, так как случайные ошибки коэффициентов будут взаимопогашаться. Модель можно использовать только для ориентировочных расчетов, т.к. она дает лишь некоторую оценку истинного значения этих величин в генеральной совокупности, а для более детального изучения влияния факторов необходимо её дальнейшее изучение.
Список использованной литературы: 1. Доугерти К. Введение в эконометрику: Пер. с англ. - М.: ИНФРА - М, 1999. - 402 с. 2. Елисеева И.И "Эконометрика": Учебник - М.: Финансы и статистика, 2001. -344 с: ил. 4. Пучков В. Ф. Решение управленческих задач средствами экономико-математического моделирования – Учебное пособие – Гатчина: Изд-во ГИЭФПТ, 2012.-53 с. 5. Эконометрика: Учебник/Под ред. И.И. Елисеевой. - м.: Финансы и статистика, 2001. - 344 с.: ил.
|

 . В данной задаче используется критерий серий, основанный на медиане выборки. Выборка признается случайной, если для 5% уровня значимости выполняются следующие неравенства:
. В данной задаче используется критерий серий, основанный на медиане выборки. Выборка признается случайной, если для 5% уровня значимости выполняются следующие неравенства: ,
,  ,
, 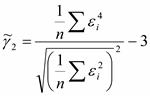 ,
,  , где γ1 и γ2 – выборочные характеристики асимметрии, а σy1 и σy2 их среднеквадратические ошибки.
, где γ1 и γ2 – выборочные характеристики асимметрии, а σy1 и σy2 их среднеквадратические ошибки. | < 1,5 σy1 , и
| < 1,5 σy1 , и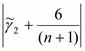 <1,5 σy1 то гипотеза о нормальном распределении принимается. В данной работе
<1,5 σy1 то гипотеза о нормальном распределении принимается. В данной работе = -0,72,
= -0,72,  =1,16, σy1 =0,47, σy2 =0,76. Гипотеза не выполняется, соответственно данная модель не отвечает второму свойству.
=1,16, σy1 =0,47, σy2 =0,76. Гипотеза не выполняется, соответственно данная модель не отвечает второму свойству. ,
,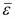 - среднее арифметическое значение, а Sɛ- стандартное среднеквадратическое отклонение для этой последовательности. Т.к расчетное t = 2,059Е-14 меньше табличного,то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.
- среднее арифметическое значение, а Sɛ- стандартное среднеквадратическое отклонение для этой последовательности. Т.к расчетное t = 2,059Е-14 меньше табличного,то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.
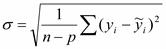
 -фактическое значение ряда
-фактическое значение ряда -теоретическое значение ряда;
-теоретическое значение ряда;