Салическая правда. где и – статические деформации пружины под действием груза D и E
где где или где Начальные условия для уравнения (1) определяются соотношениями Как известно, решение линейного дифференциального уравнения (1) складывается из общего решения и частного решения x 2 неоднородного уравнения (1) Общее решение однородного уравнения (2) имеет вид Частное решение неоднородного уравнения (3) будем искать в виде Определив производные Чтобы полученное равенство выполнялось в любой момент времени, необходимо равенство нулю выражений в квадратных скобках. Таким образом, для определения коэффициентов решение которой записывается так или после подстановки численных данных А 1 = –0.7472 см, А 2 = –0.0034 см.
Следовательно, решение уравнения (1) принимает вид причем скорость точки равна Постоянные интегрирования
Салическая правда Салическая правда (Lex Salica) является записью древних судебных обычаев салических франков, обосновавшихся на территории Римской Галлии и создавших в V—VI вв. самое крупное варварское королевство в Западной Европе. Салическая правда — не единственный сборник варварских законов и по времени записи их даже не самый древний. Но этот сборник — наиболее полный, дошедший до нас во многих списках и вариантах более раннего и более позднего времени и по содержанию отличающийся наибольшей архаичностью. В Салической правде, кроме плохого, варваризирован- ного латинского языка да счета на римские солиды и денарии, по существу, римское влияние почти совершенно не чувствуется. Перед нами выступает древнее германское право, некоторыми деталями прямо напоминающее черты быта и нравов, существовавшие у древних германцев еще за несколько сот лет до вторжения их в Римскую империю и описанные когда-то Юлием Цезарем и Тацитом. Выверено по изданию: Салическая правда. М., Образц. тип. им. Жданова, 1950. (Моск.гос.пед.ин-т им. Ленина. Ученые записки, т.LXII). Перевод Н.П.Грацианского. I. О вызове на суд 13 § 1. Если кто будет вызван на суд (ad mallum) по законам короля, и не явится, присуждается к уплате 600 денариев, что составляет 15 солидов1. § 2. Если же кто, вызвавши другого на суд, сам не явится, и если его не задержит какое-либо законное препятствие, присуждается к уплате 15 сол. в пользу того, кого он вызовет на суд. § 3. И тот, кто вызывает другого на суд, в сопровождении свидетелей должен прийти к его дому и, если последний окажется в отсутствии, должен позвать жену или кого-либо из его домашних с тем, чтобы они известили его о вызове на суд. § 4. Если же (ответчик) будет занят исполнением королевской службы, он не может быть вызван на суд. § 5. Если же он будет вне волости по своему личному делу, он 14 может быть вызван на суд, как выше упомянуто.
|

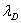 и
и  – статические деформации пружины под действием груза D и E. Изобразим грузы в промежуточном положении, отстоящем от начала координат на величину
– статические деформации пружины под действием груза D и E. Изобразим грузы в промежуточном положении, отстоящем от начала координат на величину  (точка M). Если бы верхний конец пружины был неподвижен, то в этом положении пружина была бы растянута на величину (
(точка M). Если бы верхний конец пружины был неподвижен, то в этом положении пружина была бы растянута на величину (  ). Но при смещении вниз верхнего конца пружины на некоторую величину
). Но при смещении вниз верхнего конца пружины на некоторую величину  удлинение пружины окажется меньшим на эту величину
удлинение пружины окажется меньшим на эту величину  . Следовательно, проекция силы упругости пружины на ось
. Следовательно, проекция силы упругости пружины на ось  . Проекция силы сопротивления
. Проекция силы сопротивления  . Таким образом, дифференциальное уравнение движения грузов в проекции на ось
. Таким образом, дифференциальное уравнение движения грузов в проекции на ось  ,
,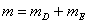 . Учитывая, что в состоянии статического равновесия грузов
. Учитывая, что в состоянии статического равновесия грузов 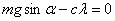 , получим
, получим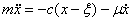 ,
, , (1)
, (1) ,
,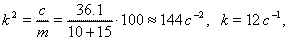

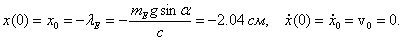
 соответствующего однородного уравнения
соответствующего однородного уравнения (2)
(2) . (3)
. (3)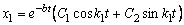 . (4)
. (4)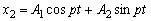 . (5)
. (5) ,
,  , подставив их в уравнение (3), получим
, подставив их в уравнение (3), получим .
. и
и  имеем систему из двух линейных уравнений
имеем систему из двух линейных уравнений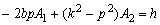 ,
,  = 0,
= 0, ,
,  ,
, 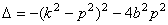 , (6)
, (6) ,
,
 .
. и
и  определим из начальных условий: С 1 = –1.2928 см, С 2 = –0.2181 см. В результате уравнение движения груза имеет вид
определим из начальных условий: С 1 = –1.2928 см, С 2 = –0.2181 см. В результате уравнение движения груза имеет вид