Особые случаи изоквант
Рассмотрим случай, когда имеет место совершенная замещаемость факторов производства. Производственная функция при этом имеет вид: Линейная функция:
Рис. 8.5. Изокванта при совершенной заменяемости факторов Тангенс угла наклона изокванты равен предельной норме технической замены неквалифицированных грузчиков квалифицированными. Еще одна производственная функция — функция Леонтьева. Она предполагает жесткую дополняемость факторов производства. Это означает, что факторы могут использоваться только в строго определенной пропорции, нарушение которой технологически невозможно.
Рис. 8.6. Изокванты в случае жесткой дополняемости факторов производства Аналитически такая производственная функция имеет вид: q = min {aK; bL}, где а и b — постоянные коэффициенты, отражающие производительность соответственно капитала и труда. Соотношение этих коэффициентов определяет пропорцию использования капитала и труда. В нашем примере с авиарейсом производственная функция выглядит так: q = min{1K; 0,2L}. Дело в том, что производительность капитала здесь составляет один рейс на один самолет, а производительность труда — один рейс на пять человек или 0,2 рейса на одного человека. Если авиакомпания располагает самолетным парком в 10 машин и имеет 40 человек летного персонала, то ее максимальный выпуск составит:q = min{ 1 х 8; 0,2 х 40} = 8 рейсов. Два самолета при этом будут простаивать на земле из-за нехватки персонала.
|

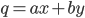 где
где  — число квалифицированных рабочих,
— число квалифицированных рабочих, 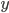 — число неквалифицированных рабочих, а и b — постоянные параметры, отражающие производительность соответственно одного квалифицированного и одного неквалифицированного рабочего. Соотношение коэффициентов а и b — предельная норма технической замены неквалифицированных грузчиков квалифицированными. Она постоянна и равна N: MRTSxy = a/b = N.
— число неквалифицированных рабочих, а и b — постоянные параметры, отражающие производительность соответственно одного квалифицированного и одного неквалифицированного рабочего. Соотношение коэффициентов а и b — предельная норма технической замены неквалифицированных грузчиков квалифицированными. Она постоянна и равна N: MRTSxy = a/b = N.




