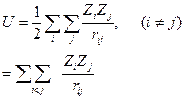Оператор энергии и уравнение Шредингера
Энергия излучаемого или поглощаемого кванта:
Частота
определяет длины волн в спектре атома водорода.
Переходы электрона с возбужденных энергетических состояний на основной энергетический уровень (
переходы на уровень с
переходы на уровень с
Теория Бора не смогла объяснить строение сложных атомов. Для объяснения поведения микрочастиц была развита квантовая механика.
Она основана на том, что любая микрочастица, наряду с корпускулярными, обладает также волновыми свойствами (гипотеза де Бройля).
Для фотона, импульс
По аналогии с фотоном, любую микрочастицу можно рассматривать как волну с длиной волны
Гипотеза де Бройля подтверждена экспериментально наблюдением дифракции электронов, а затем и протонов.
Принцип неопределенностей. Оператор энергии и уравнение Шредингера В классической механике полная энергия системы описывается функцией Гамильтона
По второму постулату, оператор полной энергии будет записываться как
или
Этот оператор называют оператором Гамильтона или гамильтонианом. Если Е – точное значение энергии системы в данном состоянии y, то по третьему постулату
откуда
или
Мы вновь пришли к знакомому уравнению Шредингера. Для системы из нескольких частиц гамильтониан записывается в виде:
где
Поэтому записать уравнение Шредингера для молекулы, например, воды, несложно. Другое дело, что с ним делать потом. Напомним, что мы уже доказывали, что операторы составляющих импульса эрмитовы. Можно показать, что самосопряженными будут и их квадраты. Таким образом, самосопряженным будет и оператор Гамильтона, а значит, его собственное значение Е всегда действительно.
|

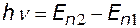 .
.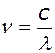 ,
,  длина волны,
длина волны, 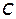 - скорость света в вакууме.
- скорость света в вакууме. =
=  +
+ 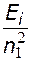 =
=  ,
, =
= 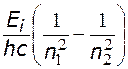 .
. - формула Бальмера,
- формула Бальмера,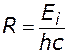 = 1,1∙107 м-1 - постоянная Ридберга.
= 1,1∙107 м-1 - постоянная Ридберга.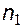 и
и  - номера энергетических состояний (номера орбит) электрона.
- номера энергетических состояний (номера орбит) электрона.

 .
.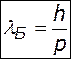 ,
,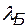 - длина волны де Бройля.
- длина волны де Бройля.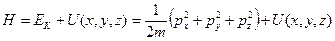



 ,
,

 ,
, – оператор Лапласа для i -й частицы, а энергия U чаще всего зависит от взаимного расположения всех частиц. В случае кулоновского взаимодействия (именно его приходится рассматривать в молекулах в отсутствие внешних полей)
– оператор Лапласа для i -й частицы, а энергия U чаще всего зависит от взаимного расположения всех частиц. В случае кулоновского взаимодействия (именно его приходится рассматривать в молекулах в отсутствие внешних полей)