Команды получения распределений и описательных статистик
3.1.1. FREQUENCIES – получение одномерных распределений переменных Процедура FREQUENCIES позволяет получить только самые основные статистические характеристики случайной переменной: перечень значений и частотное распределение, т. е. сколько раз переменная принимала каждое из этих значений. Частотное распределение выдается в числовом виде, в виде процентов и в зависимости от желания пользователя представляется в виде таблицы и/или графика. По умолчанию выдается таблица. Пример FREQUENCIES VAR V1 V8 / HISTOGRAM /STATISTICS = MEANS. Синтаксис: указываются через пробел переменные для табулирования. Допустимы числовые и строковые переменные. Параметры процедуры необязательны и задаются ключевыми словами, разделенными косыми чертами «/». В параметрах могут быть подпараметры. На рис. 3.1 и в табл. 3.1 дан пример полученного процедурой FREQUENCIES частотного распределения респондентов анкеты «Курильские острова» и его столбиковой диаграммы по результатам их ответов на вопрос о точке зрения на иностранную помощь. Наиболее распространенным (433 ответа) было мнение, что островам нужна ограниченная иностранная помощь. Из текста таблицы и подписей гистограммы видно, насколько удобно в практической работе использовать VAR LAB и VAL LAB – команды присвоения признакам текстовых имен. В колонке «Percent» проценты даны относительно всего объема выборки с учетом неопределенных кодов. В колонке «Valid Percent» приведены проценты в выборке без неопределенных кодов. В колонке «Cum Percent» – суммарный процент с нарастающим итогом, рассчитанный без учета объектов с неопределенными значениями.

Таблица 3.1 Таблица распределения числа респондентов курильского обследования
Пример MISSING VALUES V1(0). FREQUENCIES V1 /BARCHART. В выборке 5 респондентов из 721 не ответили на первый вопрос и были закодированы при наборе данных «0». В данном примере мы указываем пакету, что нулевой код следует воспринимать как неопределенные пользовательские значения. В процедуре FREQUENCIES полезно использовать следующие необязательные параметры: /BARCHART – столбиковая диаграмма; /PIECHART – круговая диаграмма; /HISTOGRAM – гистограмма; /NTILES – n -тили (квартили, квинтили, децили и др.); /PERCENTILES –процентили; /STATISTICS – все статистики, реализованные в команде. 3.1.1.1. Подкоманды /BARCHART, /PIECHART и /HISTOGRAM – диаграммы распределения Столбиковая и круговая диаграммы обычно используются для неколичественных переменных. Гистограмма необходима для графического представления количественных данных. Для ее построения SPSS подбирает интервалы группирования значений переменной и представляет графически частоты или доли числа объектов, попавших в соответствующие интервалы. К сожалению, принцип определения числа интервалов в имеющейся у нас документации SPSS не описан. В синтаксисе команды можно задать интервал значений, для которых будет выдаваться гистограмма. На рис. 3.2 представлен график, полученный командой, в которой задан интервал:
Соотношение высоты столбиков отражает соотношение количества респондентов, имеющих возраст из соответствующего двухлетнего интервала. Например, из гистограммы видим, что более всего в выборке было 36 – 38-летних. Или: с увеличением возраста после 44 лет численность опрашиваемых сокращалась почти в равных пропорциях для трех последующих интервалов. Можно отметить также активное включение в опрос лиц в возрасте 50–52 года. 3.1.1.2. Подкоманды /NTILES, /PERCENTILES – n -тили, процентили Подкоманда NTILES задает печать n -тилей – значений переменной, делящих распределение на заданное число групп с равным числом объектов. Следующая команда выдает квинтили (деление на 5 частей) переменной, содержащей данные по доходу: FREQUENCIES /VARIABLES = V14 /NTILES = 5. Подкоманда PERCENTILES печатает процентили (процентиль – это квантиль, рассчитанная по доле, указанной в процентах). Процентили являются значениями переменной, отделяющими указанную в процентах долю совокупности объектов. Пример: найдем значения дохода, отделяющие 10 % выборки, 50 % (медиану) и 90 %: FREQUENCIES /VARIABLES = V14 /PERCENTILES 10 50 90. Процентили удобно использовать, если нам нужно разбить упорядоченные значения переменной на интервалы, которые содержали бы задаваемое нами количество объектов (анкет). 3.1.1.3. Подкоманда /STATISTICS – описательные статистики Подкоманда позволяет получить одномерные описательные статистики. FREQUENCIES V1 V2 V4 /STATISTICS DEFAULT. Ключевые слова: MEAN –среднее; SEMEAN –стандартная ошибка среднего; MEDIAN– медиана (процентиль с 50 %) MODE –мода (наиболее частое значение) STDDEV –стандартное отклонение; VARIANCE –дисперсия; KURTOSIS –эксцесс (пикообразность); SEKURT – стандартная ошибка эксцесса; SKEWNESS –коэффициент асимметрии (скошенность); SESKEW –стандартная ошибка коэффициента асимметрии; RANGE –разброс = (MAX - MIN); MINIMUM –минимум; MAXIMUM –максимум; SUM –сумма всех значений переменной; ALL –все статистики; DEFAULTS –статистики МEAN, STDDEV, MIN, MAX. Статистика MEANвычисляется по известной формуле Стандартную ошибку можно использовать для оценки доверительного интервала матожидания (в случае нормального распределения генеральной совокупности границы (1 – a) ´ 100 % доверительного интервала имеют вид Примерно в пределах На практике постоянно возникает вопрос, нормально ли распределение переменной, так как многие статистические методы разработаны в предположении нормальности. Исследуемые распределения обычно отличаются от нормального закона, а в этом случае оценки некоторых параметров будут смещены. Например, будет некорректно вычислена наблюдаемая значимость оценки. Исследователю важно понять, опасно ли смещение выборочного распределения от нормального. Приближенно и быстро оценить масштабы отклонения распределения от нормального можно, используя скошенность и пико Скошенность SKEWNESS определяется расчетом третьего момента по формуле Если полученная величина меньше нуля, то распределение растянуто влево, если больше нуля – то вправо. Чем больше отличие от нуля, тем значительнее отклонения распределения от нормального. Пикообразность KURTOSIS определяется значением четвертого момента: Нулевое значение Kurtosis означает, что пикообразность распределения совпадает с пикообразностью нормального распределения. Чем больше четвертый момент, тем больше пикообразность распределения и, следовательно, отличие от нормального. В этом случае существенность отклонений статистик от теоретических можно проверить, используя стандартные ошибки этих статистик (Std. Error of Skewness и Std. Error of Kurtosis). В основе лежит факт, что отношение статистики к ее стандартной ошибке имеет распределение, близкое к нормальному). Например, если это отношение превышает 1,96, то мы должны отклонить гипотезу о равенстве Kurtosis нулю в генеральной совокупности и, следовательно, о нормальном распределении переменной. Полезность этих двух статистик не ограничивается проверкой нормальности распределения. Приобретя некоторый опыт, можно использовать эти статистики для качественного анализа распределения. Например, при исследовании доходов можно использовать Kurtosis как измеритель степени неравенства доходов населения. Чем больше пикообразность, тем однороднее доходы. Перечисленные описательные статистики команды FREQUENCIES играют в анализе данных особую роль. Они позволяют провести первый этап статистических исследований выборки. Ниже приведен пример описательных статистик, полученных для переменной «Среднемесячный душевой доход в семье», построенной по ответам на 14-й вопрос анкеты «Курильские острова». FREQUENCIES VARIABLES = V14 /NTILES = 4 /PERCENTILES = 10 90 /STATISTICS = STDDEV VARIANCE RANGE MINIMUM MAXIMUM SEMEAN MEAN MEDIAN MODE SUM SKEWNESS SESKEW KURTOSIS SEKURT. Команда вычисляет также n -тили и процентили. Таблица3.2 Статистики переменной V14 – «Душевой доход»,
|

 FREQUENCIES VARIABLES = V9/ HISTOGRAM min(30), max(50).
FREQUENCIES VARIABLES = V9/ HISTOGRAM min(30), max(50).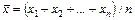 , VARIANCE – несмещенная оценки дисперсии –по формуле
, VARIANCE – несмещенная оценки дисперсии –по формуле  , SEMEAN – стандартная ошибка среднего – по формуле
, SEMEAN – стандартная ошибка среднего – по формуле  .
. ). Напомним, что доверительным интервалом параметра называется интервал со случайными границами, накрывающий значение параметра с заданной (доверительной) вероятностью. В частности, приближенными оценками границ 95 %-го двустороннего доверительного интервала для матожидания являются значения
). Напомним, что доверительным интервалом параметра называется интервал со случайными границами, накрывающий значение параметра с заданной (доверительной) вероятностью. В частности, приближенными оценками границ 95 %-го двустороннего доверительного интервала для матожидания являются значения  (истинное значение матожидания с вероятностью 0,95 находится в этих пределах).
(истинное значение матожидания с вероятностью 0,95 находится в этих пределах). должно находиться около 68 % наблюдений совокупности.
должно находиться около 68 % наблюдений совокупности.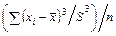 образность.
образность.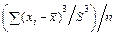 – коэффициент асимметрии.
– коэффициент асимметрии. – эксцесс.
– эксцесс.


