Cтатистики смещения частот
Реализованные в параметре CELLS статистики позволяют провести более сложный анализ связи переменных. Например, в табл. 3.4 можно увидеть, что среди полагающих ненужной иностранную помощь 12 % готовы отдать острова Японии. Среди считающих, что помощь нужна, их 37 %. В то же время в целом по совокупности лишь 15 % готовы передать острова. Существенны ли полученные отличия долей подмножеств соответственно на 3 % и 22 % от доли в целом по совокупности? Может ли в следующем обследовании связь оказаться противоположной? Основой для исследования смещения выборки от истинного распределения служат теоретические значения, ожидаемые в случае независимости выборки. Подпараметр EXPECTED параметра CELLS позволяет вывести в клетках абсолютные значения частот (Nij) и ожидаемые в предположении независимости переменных (теоретические) частоты (Eij). Отклонение (Nij – Eij) наблюдаемой частоты от ожидаемой – более удобная величина для анализа, она достаточно наглядна, но остается неясным, насколько это отклонение статистически значимо. Более полезна статистика Zij = (Nij – Eij)/σ ij – стандартизованное смещение частоты; Zij выдается в клетке при указании подпараметра ASRESID (Adjusted residuals). Иными словами, Zij представляет собой отклонение наблюдаемой частоты от ожидаемой, измеренное в числе стандартных отклонений. При этом стандартное отклонение σ ij вычисляется исходя из предположения, что Nij – случайная величина, имеющая гипергеометрическое распределение:
Если переменные независимы, то при больших N случайная величина Zij имеет нормальное распределение с параметрами (0,1). Для нее практически невероятно принять значение, большее трех стандартных отклонений, т. к. вероятность такого значения составляет менее 0,0027 (правило «трех сигм»). Поэтому, если мы получаем значение Zij, превышающее 3, то можем считать, что i -е значение и j -е значение X и Y связаны. На практике, когда анализируется единственная клетка таблицы, выставляются более слабые требования. Существенными считаются уже те односторонние отклонения, которые превышают лишь 1,65σ ij – вероятность их получения составляет 5 % . Таким образом, начиная с отклонения 1,65(Zij имеет σ ij= 1)и большего, можно высказывать гипотезу о существовании связи между значениями. (См. таблицу нормального распределения в любом статистическом справочнике). В практических расчетах принято считать теоретическое распределение Zij близким к нормальному, если К сожалению, получив данные расчетов, указывающие на зависимость (Zij > 1,96 в случае 5 %-го двустороннего критерия) значений, мы не вправе быть уверенными, что эта зависимость существует. На практике мы рассчитываем показатели значимости для множества клеток. Чем их больше, тем выше вероятность случайно получить хотя бы одно значение, превышающее указанный порог. Из теории следует, что если клетки независимы, то при критическом значении статистики Zij, равном 1,96 (5 %-й уровень значимости), мы в среднем найдем 5 «значимых» из 100 клеток таблицы. А хотя бы одну статистику, превзошедшую критическое значение (| Zij | > 1,96), в условиях независимости клеток мы можем получить с вероятностью (1 – 0,95100) = 0,9941! Таким образом, если мы получили значимые связи, то это дает нам лишь повод для высказывания гипотезы об их наличии и требует содержательной дополнительной проверки. Поэтому сложившаяся практика руководствоваться отклонением 1,96 оберегает нас только от грубейших ошибок. В то же время, если мы не получили значимых связей, то можем делать вывод либо об их отсутствии, либо о недостаточном количестве данных для их обнаружения. Величина SRESID – стандартизованное изменение частоты по сравнению с ожидаемым (Nij – Eij)/ Пример. (См. табл. 3.5.) Определим зависимость между отношением к получению иностранной помощи и «Возможностью удовлетворить территориальные требований Японии»: CROSSTABS /TABLES = v1 BY W4/CELLS = COUNT EXPECTED RESID ASRESID. Так как в CELLS указан параметр COUNT, EXPECTED, RESIDиASRESID, то в клетках выведены реальные и ожидаемые значения, а также абсолютная разность расчетной частоты от ожидаемой. В нижней строке клеток выведена эта же разность, но в числе стандартных отклонений. Таблица3. 5 Связь ответов на вопросы «Точки зрения на иностранную помощь»
В табл. 3.5 получен ответ на поставленный в начале раздела вопрос: смещение частоты в клетке «Отдать острова» – «Нужна помощь» (residual = 16) оказалось существенным, так как Z =5,5 >> 1,96! В то же время смещение частоты на 5,3 в клетке «помощь не нужна – отдать» – не значимо В статистической взаимосвязи значений переменных можно еще раз убедиться, рассмотрев табл. 3.6 с процентными распределениями (в среднем по совокупности 15 % считают, что острова можно отдать, в то время как в этой группе таковых 37 %!). В то же время, судя по статистикам, хотя и видна отрицательная связь значений «нужна ограниченная помощь» – «отдать острова», она все же не достаточно значима. Конечного потребителя полученных результатов чаще интересует не значение Z -статистик, а величина смещения процентов. Надеемся, что нам удалось показать, что эти статистики наиболее интересны для интерпретации. К сожалению, в SPSS расчет Zij реализован без учета размеров выборки, что необходимо иметь в виду, так как для малых выборок эти вероятностные рассуждения оказываются неточными. 3.2.1.4. Подкоманда /STATISTICS – исследование связи неколичественных переменных В предыдущем разделе изучалась связь отдельных значений переменных. Для получения ответа на вопрос о связи самих переменных используется подкоманда STATISTICSкоманды CROSSTABS. Пользователю необходимо указать статистику или параметр, выбранный для исследования связи переменных. Вот некоторые из этих статистик: CHISQ – позволяет оценить связь с помощью критерия хи-квадрат; кроме значения коэффициента хи-квадрат при задании этого ключевого слова выдается отношение правдоподобия (Likelihood Ratio), а также статистика для проверки линейной связи. Последняя статистика редко используется и поэтому не рассматривается в нашем учебно-методическом пособии. PHI – коэффициент фи-Пирсона; вместе с этим коэффициентом выдаются: V –коэффициент Крамера; CC – коэффициент контингенции; BTAU –тау-В Кендалла для ранговых переменных; CTAU – тау-С Стюарта для ранговых переменных; ALL –все статистики (около десятка), включая вышеперечисленные. Как можно охарактеризовать в целом связь неколичественных переменных? Для характеристики их связи наиболее часто используется критерий хи-квадрат (CHISQ), основанный на вычислении статистики: CHISQ = Эта величина показывает расстояние эмпирически полученной (расчитанной нами по результатам обследования на основании выборки) таблицы сопряженности от ожидаемой теоретически. В ее основе лежит расстояние между значениями Nij выборочной таблицы и Eij – ожидаемыми в условиях независимости переменных. Само по себе значение статистики ни о чем не говорит. Важно знать вероятность получения расстояния CHISQ, большего, чем оно может быть для случайной выборки в условиях независимости переменных. Напомним, что такая вероятность называется наблюдаемой значимостью и обозначается словом Significance (возможны сокращения Sig., P- значения). Пакет выдает выборочное значение CHISQ и его значимость. Традиционно считается, что значение Significance,меньшее 0,05, свидетельствует о взаимосвязи переменных, т. к. значение статистики попадает в критическую область и гипотезу о независимости переменных следует отвергнуть. CHISQ в условиях независимости и при достаточном числе наблюдений имеет распределение, близкое к распределению хи-квадрат с (r – 1) (c – 1) степенями свободы, где r – число строк в таблице, с – число столбцов (CHISQ теор. »c2((r – 1) (c – 1))). Существует эмпирическое правило, по которому считается, что CHISQ достаточно точно аппроксимируется теоретическим распределением c2((r – 1) (c – 1)), если не более 20 % клеток имеют ожидаемые частоты Eij < 5 и нет Eij < 1. В выдаче всегда присутствует информация о числе клеток, где это соотношение не выполняется. Рекомендуется использовать в CROSSTABS критерий хи-квадрат для переменных с небольшим числом значений, что достигается перекодировкой переменных. Вместе с критерием хи-квадрат выдается также логарифм отношения правдоподобия LI:
Этот показатель также имеет асимптотическое хи-квадрат – распределение, но более устойчивое к объему выборки. Поэтому при оценке связи пары признаков мы рекомендуем пользоваться отношением правдоподобия. Таблица3. 6 Тесты хи-квадрат
a 0 cells (.0 %) have expected count less than 5. The minimum expected count is 22,25. Наблюдаемая значимость (Significance ) – это вероятность случайно получить большее значение, чем выборочное. Таким образом, для CHISQ наблюдаемая значимость (SIG) равна P { CHISQ > CHISQ выбороч.}, и, аналогично, для отношения правдоподобия LI наблюдаемая значимость (SIG) равна P { LI > LI выбороч.}. Пример задания для исследования связи ответа на вопрос о необходимости иностранной помощи(v1) и полом (v8): CROSSTABS v8 BY v1 /CELLS COUNT ROW COL ASRESID /STATISTICS = CHISQ. В приведенном примере наблюдаемая значимость CHISQ составила около 1,5 % (см. Asymp. Sig. (2-sided)), значимость LI примерно 1,3 %. С такой незначительной вероятностью в условиях независимости можно случайно получить большие значения соответствующих статистик. Поэтому в соответствии с 5 %-м уровнем значимости переменные v8 и v1 следует считать связанными (1,5 % < 5 %). Таким образом, можно сделать вывод, что мужчины и женщины имеют разные мнения в вопросе об иностранной помощи. Текст под таблицей «a 0 cells (.0 %) have expected count less than 5. The minimum expected count is 22,25» свидетельствует, что все ожидаемые частоты больше 5, их минимум равен 22,25. Это свидетельствует о корректности использования критерия. В расчетах нами было получено для клетки «мужчины» – «помощь нужна», значение Z -статистики, равное 2,9, что больше 1,65, и, следовательно, ответы зависимы. Кроме того, из таблицы следует, что о необходимости помощи говорят вдвое больше мужчин, чем женщин. Мы не будем приводить здесь эту таблицу, покажем лишь столбиковую диаграмму на рис. 3.4, полученную командой
На диаграмме ясно видно, что среди респондентов, сказавших, что помощь нужна, столбик, соответсвующий количеству мужчин, существенно больше столбика, соответствующего количеству женщин.
|

 .
.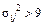 . Хотя последнее ограничение достаточно жестко, так как можно показать, что для его выполнения в выборке должно быть по крайней мере 144 наблюдения.
. Хотя последнее ограничение достаточно жестко, так как можно показать, что для его выполнения в выборке должно быть по крайней мере 144 наблюдения. – связана с распределением Пуассона. Напомним, что распределение Пуассона – это распределение числа успехов для редко случающихся событий при большом числе испытаний. Если попадание наблюдения в клетку (i,j) считать этим редким событием, то ожидаемое значение
– связана с распределением Пуассона. Напомним, что распределение Пуассона – это распределение числа успехов для редко случающихся событий при большом числе испытаний. Если попадание наблюдения в клетку (i,j) считать этим редким событием, то ожидаемое значение  можно считать оценкой параметра распределения Пуассона (l). Дисперсия распределения Пуассона совпадает с его математическим ожиданием, поэтому (Nij – Eij)/
можно считать оценкой параметра распределения Пуассона (l). Дисперсия распределения Пуассона совпадает с его математическим ожиданием, поэтому (Nij – Eij)/  .
. .
. CROSSTABS v8 BY v4 / CELLS COUNT ROW COL ASRESID /BARCHART.
CROSSTABS v8 BY v4 / CELLS COUNT ROW COL ASRESID /BARCHART.


