CELLS статистики смещения частот
Реализованные в параметре CELLS статистики позволяют провести более сложный анализ связи переменных. Например, в таблице 3.4 можно увидеть, что среди считающих, что иностранная помощь не нужна, 12% готовы отдать острова Японии, а среди считающих, что помощь нужна - их 37%. В то же время, в целом по совокупности 15% готовы передать острова. Существенны ли отличия от долей в целом по совокупности на 3% и 22%? Может ли в следующем обследовании связь оказаться противоположной? Основой для исследования смещения выборки от истинного распределения служат значения, ожидаемые в случае независимости выборки. Подпараметр EXPECTED параметра CELLS позволяет вывести в клетках абсолютные значения частот (Nij), ожидаемых в случае независимости соответствующих клетке значений переменных. Отклонение (Nij - Eij) наблюдаемой частоты от ожидаемой - более удобная величина для анализа: она достаточно наглядна, но неясно, насколько она статистически значима. Более полезна статистика Zij =(Nij - Eij)/ σij - стандартизованное смещение частоты; Zij выдается в клетке при указании подпараметра ASRESID (Adjusted residuals). Иными словами, Zij представляет собой отклонение наблюдаемой частоты от ожидаемой, измеренное в числе стандартных отклонений. При этом стандартное отклонение вычисляется исходя из предположения, что Nij это случайная величина, имеющая гипергеометрическое распределение:
Если переменные независимы, то, при больших N, случайная величина Zij имеет нормальное распределение с параметрами (0,1). Для нее практически невероятно отклонение, большее трех стандартных отклонений, т.к. вероятность такого значения составляет менее 0.0027 (правило "трех сигм"). Поэтому, если мы получаем значение Zij, превышающее 3, то можем считать, что i -ое значение и j -ое значения X и Y связаны. На практике нередко, когда анализируетсся единственная клетка таблицы, выставляются более слабые требования. Существенными считаются односторонние отклонения, которые превышают 1,65σij - вероятность их получения составляет 5%. Таким образом, начиная с отклонения 1,65σij и большего, можно уже высказывать гипотезу о существовании связи между значениями (см. таблицу нормального распределения в любом статистическоим справочнике). Эмпирическим критерием, когда распределение Zij близким к нормальному, следует считать является соотношение для дисперсии Следует заметить, что в действительности мы имеем дело с множеством статистик значимости и, при переборе их, велика вероятность случайно получить их значения, превышающие указанные пороги. Если бы клетки были независимы, при критическом значении статистики Zij, равном 1.96 (5% уровень значимости) мы в среднем в условиях независимости данных находили бы 5 "значимых" из 100 клеток таблицы, а хотя бы одну статистику, Zij >1.96 мы можем получить с вероятностью (1-0.95100)=0.9941! Поэтому сложившаяся практика руководствоваться отклонением 1.65 σij оберегает нас только от грубейших ошибок. Таблица 3.5. Связь "Точки зрения на иностранную помощь" и "Возможностью удовлетворить территориальные требований Японии" (статистики смещений частот)
Величина SRESID - стандартизованное изменение частоты по сравнению с ожидаемым (Nij - Eij)/ Пример. Определим зависимость между отношением к получению иностранной помощи и "Возможностью удовлетворить территориальные требований Японии": CROSSTABS /TABLES=v1 BY W4/CELLS=COUNT expected resid asresid. Так как в CELLS указан параметр COUNT, expected, resid и asresid, то в клетках выведены реальные и ожидаемые значения, а также абсолютная разность расчетной частоты от ожидаемой, и затем эта же разность, но в числе стандартных отклонений. В таблице 3.5 получен ответ на поставленный в начале раздела вопрос: смещение частоты в клетке "Отдать острова" - "Нужна помощь" (residual=16) оказалось существенным, Z=5.5, в то же время смещение частоты на 5.3 в клетке "помощь не нужна - отдать" - не значимо (Z=1.3). Кроме того, в полученной значимой связи можно еще раз убедиться, рассмотрев таблицу 6 с процентными распределениями (в среднем по совокупности 15% считают, что острова можно отдать, в то время как в этой группе таковых 37%!). В то же время, судя по статистикам, хотя видна отрицательная связь значений "нужна ограниченная помощь" - "отдать острова", она не достаточно значима. Надеемся, что нам удалось показать, что эти статистики наиболее интересны для интерпретации. К сожалению, в SPSS расчет
|

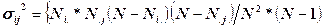
 . Хотя последнее ограничение достаточно жестко.
. Хотя последнее ограничение достаточно жестко. - связана с распределением Пуассона. Напомним, что распределение Пуассона - это распределение числа успехов для редко случающихся событий при большом числе испытаний. Если попадание наблюдения в клетку (i,j) считать этим редким событием, то ожидаемое значение
- связана с распределением Пуассона. Напомним, что распределение Пуассона - это распределение числа успехов для редко случающихся событий при большом числе испытаний. Если попадание наблюдения в клетку (i,j) считать этим редким событием, то ожидаемое значение 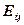 можно считать оценкой параметра распределения Пуассона. Дисперсия распределения Пуассона совпадает с его математическим ожиданием, отсюда (Nij - Eij)/
можно считать оценкой параметра распределения Пуассона. Дисперсия распределения Пуассона совпадает с его математическим ожиданием, отсюда (Nij - Eij)/  реализован без учета размеров выборки, что необходимо иметь в виду, так как для малых выборок эти вероятностные рассуждения оказываются неточными.
реализован без учета размеров выборки, что необходимо иметь в виду, так как для малых выборок эти вероятностные рассуждения оказываются неточными.


