Уравнение радиального равновесия. Условия связи между составляющими скорости на различных радиусах.
Для определения изменения параметров по радиусу лопаточного венца компрессора необходимо использовать метод, изложенный в гл. 5. Ниже для наглядности преимуществ и недостатков применяемых методов расчета распределения параметров потока по радиусу воспользуемся упрощенными соотношениями теории цилиндрической ступени, считая жидкость несжимаемой, не учитывая потерь и принимая величину H *= f (r)=const. Из упрощенного уравнения радиального равновесия и уравнения Бернулли - однозначная связь между законами изменения окружной и осевой компонент абсолютной скорости: Для определения изменения са для закона постоянной реактивности воспользуемся формулой (6.10): cu = u (1–)– H т/(2 u). (6.23) Подставляем выражение (6.23) при =const и H т=const в уравнение (6.22) и получим для закона постоянной реактивности Поскольку в формуле (6.23) =const, H т=const, u = r, то: cu = Аr + В / r (6.25) где А и В – постоянные величины. Для случая H т=const при А =0 соотношение (6.25) дает закон закрутки cur =const; при В =– Таким образом, зная сu, са и величину окружной скорости на каждом радиусе проточной части, можно построить треугольники скоростей и определить все параметры ступеней. Т.к. H т= f (r)=const, то
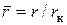 , а окружные и осевые компоненты скорости отнесены к uк.
|
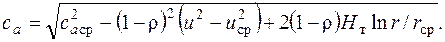(6.24)
/2 – закон постоянства циркуляции.
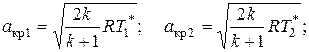
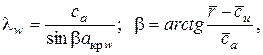
=0,5):
а – периферийный радиус; б – средний; в – втулки
