Решение. а) Преобразуем уравнение, получаем Значит, или где
а) Преобразуем уравнение, получаем
б) Отметим решения на тригонометрической окружности. Отрезку
Ответ: а) б) 5. C 1. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку
Вариант № 3719547 1. C 1. а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Запишем уравнение в виде:
Значит, б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа
Замечание. Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т.п.
Ответ: а) б) 2. C 1. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку Решение.
откуда б) При помощи тригонометрической окружности отберем корни уравнения, принадлежащие промежутку Ответ: а) 3. C 1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение.
Значит, или б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие отрезку
Ответ: а) 4. C 1. Решите уравнение
|

 Значит,
Значит,  или
или  где
где  В первом случае
В первом случае  во втором случае
во втором случае  где
где 
 принадлежат корни
принадлежат корни  и
и 







 откуда
откуда 





 а) Преобразуем уравнение:
а) Преобразуем уравнение:



 б)
б) 
 .
.
 а) Запишем уравнение в виде:
а) Запишем уравнение в виде:
 , откуда
, откуда  ,
,  , или
, или  откуда
откуда 

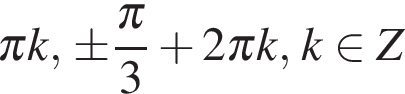 ; б)
; б)  .
.


