Решение. Произведение двух выражений равно нулю, если хотя бы одно из них равно нулю, а другое при этом не теряет смысла:
Произведение двух выражений равно нулю, если хотя бы одно из них равно нулю, а другое при этом не теряет смысла:
Поскольку Ответ:
5. C 1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку
Вариант № 3742368 1. C 2. В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 сторона основания равна 11, а боковое ребро AA 1=7. Точка K принадлежит ребру B 1 C 1 и делит его в отношении 8:3, считая от вершины B 1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D и K. Решение. Пусть L — точка, в которой плоскость сечения пересекает ребро C 1 D 1. Отрезок KL параллелен диагонали BD. Искомое сечение — трапеция BDLK (рис. 1). Плоскость сечения пересекает нижнее основание по прямой BD, параллельной B 1 D 1, значит, KL параллельно B 1 D 1.
Треугольники LC 1 K и D 1 C 1 B 1 подобны, следовательно,
Значит,
В равных прямоугольных треугольниках DD 1 L и BB 1 K имеем
Пусть LH — высота трапеции BDLK, проведённая к основанию BD (рис. 2), тогда:
Ответ: 2. C 2. Точка Решение.
В прямоугольном треугольнике
В прямоугольном треугольнике
В треугольнике
откуда Ответ:
Примечание. Ответ может быть представлен и в другом виде:
3. C 2. Дана правильная четырёхугольная пирамида MABCD, рёбра основания которой равны
|


 , то
, то  . Поэтому
. Поэтому 
 .
.




 значит, трапеция BDLK равнобедренная.
значит, трапеция BDLK равнобедренная.



 — середина ребра
— середина ребра  куба
куба  Найдите угол между прямыми
Найдите угол между прямыми  и
и 
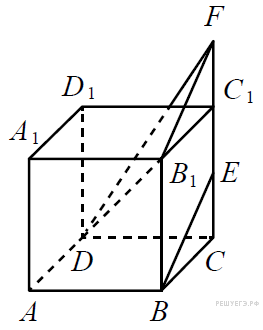 Примем ребро куба за
Примем ребро куба за  Тогда
Тогда  Проведём через точку
Проведём через точку  прямую, параллельную
прямую, параллельную  Она пересекает продолжение ребра
Она пересекает продолжение ребра  причём
причём  Искомый угол равен углу
Искомый угол равен углу  (или смежному с ним).
(или смежному с ним). с прямым углом
с прямым углом 

 с прямым углом
с прямым углом 


 а тогда
а тогда 
 .
.
 . Тангенс угла между прямыми DM и AL равен
. Тангенс угла между прямыми DM и AL равен  , L — середина ребра MB. Найдите высоту данной пирамиды.
, L — середина ребра MB. Найдите высоту данной пирамиды.


