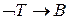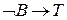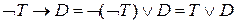Примеры программ логического доказательства
Рассмотрим задачу 1. Кто из учеников A, B, C и D играет, а кто не играет в шахматы, если известно, что: 1) Если A или B играет, то C не играет. 2) Если B не играет, то играют C и D. 3)С играет.
Пусть высказывание P истинно, если ученик P играет в шахматы. Условия 1-3 истинны, т.е. значения этих выражений равны единице. В этом случае мы приходим к системе логических уравнений:
Составим таблицу истинности для этих двух выражений: Таблица 2. Неполная таблица истинности для задачи 1
Так как из условия известно, что ученик C играет, то в данном случае достаточно рассмотреть неполную таблицу истинности, а именно только те случаи, когда Также пользуясь результатами таблицы истинности можно, можно написать небольшую программу на CLIPS, которая представляет наши вычисления в виде манипуляций фактами по определенным правилам. В начале программы у нас всего один факт - ученик C играет в шахматы: (deffacts situation (C is playing chess) ) Из табилцы истинности видно, что если (defrule rule_1 (C is playing chess) => (assert (A isn't playing chess)) (assert (B isn't playing chess)) ) Из таблицы истинности и уравнения (2) видно, что если B ложь, то истинны C и D, если C или D ложно, то B истинно. При других вариантах значений A, B, C выражение либо ложно, либо вызывает неопределенность, например, из фактов, что C и D истинны не возможно определить истинно B или ложно. Выпишем два соответствующих правила: (defrule rule_2_B_is_false (B isn’t playing chess) => (assert (D is playing chess)) )
(defrule rule_2_D_is_false (D isn't playing chess) => (assert (B is playing chess)) ) Конечно, правило rule_2_D_is_false никогда не выполнится, так как в программе нет правил, которые порождали бы факт, соответствующий продукции данного правила, но оно приведено в данном примере для полноты решения поставленной задачи в CLIPS. Программа останавливается, когда про всех учеников что-нибудь выяснено: (defrule stop (A? playing chess) (B? playing chess) (C? playing chess) (D? playing chess) => (halt) ) Полный текст программы представлен в листинге 2.
Листинг 2. Программа задачи 1. «кто играет в шахматы?» ;;из условия известно, что C - играет (deffacts situation (C is playing chess) )
;;из первого высказывания и факта, что C – играет выясняем, ;;что A и B не играют (defrule rule_1 (C is playing chess) => (assert (A isn't playing chess)) (assert (B isn't playing chess)) )
;;из второго высказывания и факта, что B не играет выяснаем, ;;что D играет (С – играет, известно из условия) (defrule rule_2_B_is_false (B isn’t playing chess) => (assert (D is playing chess)) )
;;из второго высказывания и факта, что D не играет выяснаем, ;;что B играет (С – играет, известно из условия) ;;данное правило выполняться не будет никогда!!!! (defrule rule_2_D_is_false (D isn't playing chess) => (assert (B is playing chess)) )
;;останавливаемся после того, когда все про всех выясним (defrule stop (A? playing chess) (B? playing chess) (C? playing chess) (D? playing chess) => (halt) )
Рассмотрим задачу 2. Угон машины. Следователь допрашивает 4-х гангстеров по делу о похищении автомобиля. Джек: Если Том не угонял автомобиль, то его угнал Боб Боб: Если Джек не угонял, то его угнал Том Фред: Если Том не угонял, то его угнал Джек Том: Если Боб не угонял, то его угнал я Выяснилось, что Боб солгал, а Том сказал правду. Правдивы ли показания Джека и Фреда? Кто угнал машину? Представим данные высказывания в виде логических выражений, где D, B, F, T – Джек, Боб, Фред и Том соответственно: Джек: Боб: Фред: Том: Используя представление импликации через дизъюнкцию и отрицание (25) (см. п. 3.1.1) можно убедиться, что показания Джека и Тома, Боба и Фреда эквивалентны: Джек: Том: Боб: Фред: Воспользуемся этим при написании программы на CLIPS. Для решения данной задачи создадим шаблон: (deftemplate gangster (slot name (type SYMBOL)) (slot guilty (type SYMBOL) (default Unk)) (slot truthful (type SYMBOL) (default Unk)) ) В слоте name будет хранится имя подозреваемого, guilty будет определять виновен или нет (соответствие истинным или ложным значениям простого высказывания), truthful – определяет правдиво или ложно показание. Слоты guilty и truthful по умолчанию определяется как Unk, что означает неопределенность. В дальнейшем это будет использовано, чтобы исключить повторное выполнение правил, если значение соответствующего слота уже было определено (Yes или No). Используя полученный шаблон составим базу фактов в соответствии с условием задачи: (deffacts content (gangster (name Jack)) (gangster (name Bob)(truthful No)) (gangster (name Fred)(guilty No)) (gangster (name Tom)(truthful Yes)) ) Во всех четырех высказывания фигурируют только имена Тома, Джека и Боба. Следовательно, без нарушения условия задачи можно установить, что Фред не виновен – (gangster (name Fred)(guilty No)). Так как показания Джека и Тома эквивалентны, то рассмотрим их вместе. Если Джек или Том говорит правду и Том невиновен, то виновен Боб, если не виновен Боб, то виновен – Том. Соответствующие правила будут следующие: (defrule Jack_Tom_truthful_Tom_not_guilty (gangster (name Jack|Tom) (truthful Yes)) (gangster (name Tom) (guilty No)) ?Bob<-(gangster(name Bob) (guilty Unk)) => (modify?Bob(guilty Yes)) )
(defrule Jack_Tom_truthful_Bob_not_guilty (gangster (name Jack|Tom) (truthful Yes)) (gangster (name Bob) (guilty No)) ?Tom<-(gangster(name Tom) (guilty Unk)) => (modify?Tom(guilty Yes)) ) Обратите внимание, что в первой предпосылке данных правил в слоте name используется связка |, что означает истинность предпосылки если в базе будет факт у которого значение слота name будет иметь значение Jack или Tom и truthful – Yes. Если Том или Джек сказали не правду, то Том и Боб не виновны: (defrule Jack_Tom_not_truthful (gangster (name Jack|Tom) (truthful No)) ?X<-(gangster (name Bob|Tom) (guilty Unk)) => (modify?X(guilty No)) ) В данном правиле также используется связка | в обоих предпосылках. Данное правило применимо как для Боба, так и Тома, если значение слота guilty равно Unk у соответствующих фактов. Других правил на основании высказываний Джека и Тома и известных фактов о виновности или невиновности Тома и Боба построить не возможно, так как они несут неопределенность. Например, Если известно, что Джек или Том сказали правду и Том виновен, Боб может быть как виновен, так и невиновен, и наоборот: если Боб виновен, то виновность Тома из показаний Джека и Тома определить не возможно. Аналогично выводятся правила относительно показаний Боба и Фреда: (defrule Bob_Fred_truthful_Jack_not_guilty (gangster (name Bob|Fred) (truthful Yes)) (gangster (name Jack) (guilty No)) ?Tom<-(gangster(name Tom) (guilty Unk)) => (modify?Tom(guilty Yes)) )
(defrule Bob_Fred_truthful_Tom_not_guilty (gangster (name Bob|Fred) (truthful Yes)) (gangster (name Tom) (guilty No)) ?Jack<-(gangster(name Jack) (guilty Unk)) => (modify?Jack(guilty Yes)) )
(defrule Bob_Fred_not_truthful (gangster (name Bob|Fred) (truthful No)) ?X<-(gangster (name Jack|Tom) (guilty Unk)) => (modify?X(guilty No)) ) Все предыдущие правила основывались на том, что истинность или ложность высказываний известна, но в задаче есть высказывания, истинность или ложность которых необходимо установить. Для этого составим соответствующие правила: (defrule Jack_Tom_is_truthful ?X<-(gangster(name Jack|Tom) (truthful Unk)) (gangster(name Tom|Bob) (guilty Yes)) => (modify?X(truthful Yes)) )
(defrule Jack_Tom_is_not_truthful ?X<-(gangster(name Jack|Tom) (truthful Unk)) (gangster(name Tom) (guilty No)) (gangster(name Bob) (guilty No)) => (modify?X(truthful No)) )
(defrule Bob_Fred_is_truthful ?X<-(gangster(name Bob|Fred) (truthful Unk)) (gangster(name Tom|Jack) (guilty Yes)) => (modify?X(truthful Yes)) )
(defrule Bob_Fred_is_not_truthful ?X<-(gangster(name Bob|Fred) (truthful Unk)) (gangster(name Tom) (guilty No)) (gangster(name Jack) (guilty No)) => (modify?X(truthful No)) ) Данные правила построены в соответствии с логическими выражениями, построенными на высказываниях из условия задачи. Например, показания Тома и Джека истины, если виновен Том или Боб, а если Тим и Боб не виновны, то Том и Джек сказали неправду. Если про всех все известно, то программа прекращает работу: (defrule stop (gangster (name Jack) (guilty ~Unk) (truthful ~Unk)) (gangster (name Bob) (guilty ~Unk) (truthful ~Unk)) (gangster (name Fred) (guilty ~Unk) (truthful ~Unk)) (gangster (name Tom) (guilty ~Unk) (truthful ~Unk)) => (halt) ) Полный текст программы приведен в листинге 3.
Листинг 3. Программа решения задачи 2. «Кто угнал автомобиль?» ;;шаблон (deftemplate gangster (slot name (type SYMBOL));;имя (slot guilty (type SYMBOL) (default Unk));;виновность (slot truthful (type SYMBOL) (default Unk));;истинно ли высказывание )
;;вводятся факты в соответствии с условием задачи (deffacts content (gangster (name Jack)) (gangster (name Bob)(truthful No)) (gangster (name Fred)(guilty No));;Фред не участвовал (gangster (name Tom)(truthful Yes)) )
;;останавливаемся когда про всех все известно (defrule stop (gangster (name Jack) (guilty ~Unk) (truthful ~Unk)) (gangster (name Bob) (guilty ~Unk) (truthful ~Unk)) (gangster (name Fred) (guilty ~Unk) (truthful ~Unk)) (gangster (name Tom) (guilty ~Unk) (truthful ~Unk)) => (halt) )
;;в соответствии с показаниями Джека и Тома
(defrule Jack_Tom_truthful_1 (gangster (name Jack|Tom) (truthful Yes)) (gangster (name Tom) (guilty No)) ?Bob<-(gangster(name Bob) (guilty Unk)) => (modify?Bob(guilty Yes)) )
(defrule Jack_Tom_truthful_2 (gangster (name Jack|Tom) (truthful Yes)) (gangster (name Bob) (guilty No)) ?Tom<-(gangster(name Tom) (guilty Unk)) => (modify?Tom(guilty Yes)) )
(defrule Jack_Tom_not_truthful (gangster (name Jack|Tom) (truthful No)) ?X<-(gangster (name Bob|Tom) (guilty Unk)) => (modify?X(guilty No)) )
;;в соответствии с показаниями Боба и Фреда
(defrule Bob_Fred_truthful_1 (gangster (name Bob|Fred) (truthful Yes)) (gangster (name Jack) (guilty No)) ?Tom<-(gangster(name Tom) (guilty Unk)) => (modify?Tom(guilty Yes)) )
(defrule Bob_Fred_truthful_2 (gangster (name Bob|Fred) (truthful Yes)) (gangster (name Tom) (guilty No)) ?Jack<-(gangster(name Jack) (guilty Unk)) => (modify?Jack(guilty Yes)) )
(defrule Bob_Fred_not_truthful (gangster (name Bob|Fred) (truthful No)) ?X<-(gangster (name Jack|Tom) (guilty Unk)) => (modify?X(guilty No)) )
;;Выясняем кто говорит правду, а кто нет
(defrule Jack_Tom_is_truthful ?X<-(gangster(name Jack|Tom) (truthful Unk)) (gangster(name Tom|Bob) (guilty Yes)) => (modify?X(truthful Yes)) )
(defrule Jack_Tom_is_not_truthful ?X<-(gangster(name Jack|Tom) (truthful Unk)) (gangster(name Tom) (guilty No)) (gangster(name Bob) (guilty No)) => (modify?X(truthful No)) )
(defrule Bob_Fred_is_truthful ?X<-(gangster(name Bob|Fred) (truthful Unk)) (gangster(name Tom|Jack) (guilty Yes)) => (modify?X(truthful Yes)) )
(defrule Bob_Fred_is_not_truthful ?X<-(gangster(name Bob|Fred) (truthful Unk)) (gangster(name Tom) (guilty No)) (gangster(name Jack) (guilty No)) => (modify?X(truthful No)) )
Варианты заданий 1. В школе было разбито стекло. В содеянном были заподозрены четыре ученика: Миша, Леня, Толя и Дима. Вот что они сказали в кабинете директора: Леня: Я не виноват. Я даже не подходил к окну. Миша знает, кто это сделал. Дима: Стекло разбил не я. С Мишей я не был знаком до поступления в школу. Это сделал Толя. Толя: Я не виновен. Это сделал Миша. Дима говорит неправду, утверждая, что я разбил стекло. Миша: Я не виноват. Стекло разбил Леня. Дима может поручиться за меня, т.к. знает меня очень давно. При дальнейших расспросах ребята сознались, что 2 фразы из сказанных ими – истинны, а одна, соответственно, ложна. Требуется выяснить, кто разбил стекло. 2. Определите, кто из подозреваемых участвовал в преступлении, если известно: a) если Иванов не участвовал или Петров участвовал, то Сидоров участвовал; b) если Иванов не участвовал, то Сидоров не участвовал. 3. Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо знавший ребят, высказал предположения: a) Аня пойдет в кино только тогда, когда пойдут Вика и Сергей; b) Аня и Сергей пойдут в кино вместе или же оба останутся дома; c) чтобы Сергей пошел в кино необходимо чтобы пошла Вика. Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино? 4. Виктор, Роман, Леонид и Сергей заняли на олимпиаде по физике четыре первых места. Когда их спросили о распределении мест, они дали три ответа: a) Сергей – первый, Роман – второй; b) Сергей – второй, Виктор – третий; c) Леонид – второй, Виктор – четвертый. Известно, что в каждом ответе только одно утверждение истинно. Как распределились места? 5. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения: Алеша: Это сосуд греческий и изготовлен в V веке. Боря: Это сосуд финикийский и изготовлен в III веке. Гриша: Это сосуд не греческий и изготовлен в IV веке. Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд? 6. В нарушении правил обмена валюты подозреваются четыре работника банка – A, B, C, D. Известно, что: a) если A нарушил, то и B нарушил правила обмена валюты; b) если B нарушил, то и C нарушил или A не нарушал; c) если D не нарушил, то A нарушил, а C не нарушал; d) если D нарушил, то и A нарушил. Кто из подозреваемых нарушил правила обмена валюты? 7. Богданову, Демидову и Смирнову предъявлено обвинение в ограблении ювелирного магазина. С места преступления они скрылись на автомобиле. На следствии Богданов сказал, что они уехали на синем «Москвиче», Демидов сказал, что это была черная «Волга», Смирнов утверждал, что это были «Жигули», но не синие. Известно, что каждый из них правильно назвал либо марку автомобиля, либо цвет. Определите марку автомобиля и ее цвет. 8. Четыре подруги Аня, Маша, Настя, Вика пришли в магазин. Продавец сказал, что осталось только четыре платья: Красное, Розовое, Оранжевое, Синее. a) Красное платье купила Аня, а розовое – Маша; b) Аня взяла розовое платье, а Вика купила оранжевое; c) Настя забрала розовое, а Вика – синее платье. Кто купил синее платье и какое платье выбрала Вика, если известно, что половина каждого утверждения истинна, а половина – ложь. 9. В олимпиаде по биологии участвовало пять девушек: Алла, Нина, Вика, Рита, Соня. Об итогах олимпиады имеется пять высказываний: a) первое место заняла Алла, а Рита оказалась третьей; b) пятой была Вика, а вот Нина поднялась на первое место; c) первое место заняла Соня, а вот Вика была второй; d) Рита на последнем, пятом, месте, а Нина была предпоследней; e) Нина была четвертой, а первой – Алла. Кто занял первое место и на каком месте была Алла, если известно, что в каждом высказывании одно утверждение правильное, а другое – нет. 10. Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров: a) Макс победит, Билл – второй; b) Билл – третий, Ник – первый; c) Макс – последний, а первый – Джон. Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. 11. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто – нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля: Я всегда прогуливаю астрономию. Не верьте тому, что скажет Саша. Саша: Это был мой первый прогул этого предмета. Миша: Все, что говорит Коля – правда. Определите, кто из них кто. 12. Однажды Алиса повстречала Льва и Единорога, отдыхавших под деревом. Странные это были существа. Лев лгал по понедельникам, вторникам и средам и говорил правду во все остальные дни недели. Единорог же вел себя иначе: он лгал по четвергам, пятницам и субботам и говорил правду во все остальные дни недели. Они высказали следующие утверждения: Лев: «Вчера был один из дней, когда я лгу». Единорог: «Вчера был один из дней, когда я тоже лгу». Из этих двух высказываний Алиса сумела вывести, какой день недели был вчера. Что это был за день? 13. Покупатель в каждом из магазинов A, B, C и D сделал по одной покупке и приобрел джойстик, дискеты, бумагу и картридж. Известно, что: a) джойстик и картридж купил не в A; b) в C зашел когда уже купил дискеты и бумагу; c) в D не было ни картриджа, ни дискет; d) в B приехал, когда джойстик уже был куплен; e) из D уходил без джойстика. Необходимо определить в каком магазине были куплены дискеты. 14. Три подразделения A, B, C компании хотят получить по итогам квартала максимальную прибыль. Были сделаны следующие прогнозы: a) если A получит максимальную прибыль, то максимальную прибыль получат также B и C; b) либо A и C получат максимальную прибыль одновременно, либо одновременно не получат; c) для того, чтобы C получило максимальную прибыль, необходимо, чтобы и B получило максимальную прибыль. По завершении квартала оказалось, что один из трех прогнозов ложен. Какие из названных подразделений получили максимальную прибыль? 15. Есть 2 комнаты. В каждой из комнат будет находиться либо принцесса, либо тигр, хотя вполне может статься, что сразу в обеих комнатах обнаружится по тигру или там окажутся одни лишь принцессы. Уздник должен угадать, кто находится в каждой комнате. Если он угадает, то женится на принцессе, если нет, то его растерзает тигр. На табличках, прикрепленных к дверям каждой из комнат, написано: I. В этой комнате находится принцесса, а в другой комнате сидит тигр II. В одной из этих комнат находится принцесса; кроме того, в одной из этих комнат сидит тигр Причем, известно, что на одной табличке написана правда, а на другой – ложь. А вы на месте узника, какую бы дверь открыли? 16. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку: «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу известно только, что надписи либо истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики. 17. Фамилии командира взвода, заместителя командира взвода и командиров трех отделений – Антипов, Борисов, Васильев, Григорьев, Дмитриев. Фамилии командиров первого и второго отделений начинаются на F и L и они решили подружиться. Дмитриев недавно узнал, что командир взвода и командир второго отделения – двоюродный братья. Григорьев дружит с командиром и его заместителем. У Васильева нет двоюродных братьев. Определите фамилии командира, заместителя командира и командиров отделений.
4. Лабораторная работа №3. Реализация эвристических поисковых алгоритмов на примере алгоритма А*
|

 (1)
(1) (2)
(2) (3)
(3)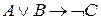

 ,
,  ,
,  .
.