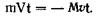Маховые упражнения
Подавляющее большинство упражнений на снарядах — маховые. Эти упражнения ценны тем, что совершенствуют координационные спо-
собности, умение ориентироваться в пространстве. Маховые упражнения — это вращательные движения по кругу или его частям. Вращательные движения связаны с понятием «ось». Оси, вокруг которых вращается спортсмен, могут быть действительными (например, гриф перекладины или жердь брусьев разной высоты) и воображаемыми (например, линия, соединяющая точки хвата на кольцах или параллельных брусьях) при поперечном положении плечевой оси гимнаста по отношению к оси жерди. По отношению к телу гимнаста оси называются: фронтальная, сагиттальная, продольная. Все эти оси являются воображаемыми (рис. 74). Они перпендикулярны друг другу и пересекаются в одной точке — ц.т.т. спортсмена. Это главные центральные оси инерции. Зна- ние закономерностей вращения вокруг этих осей особенно важно для таких видов спорта, как спортивная гимнастика, прыжковая акробатика, прыжки в воду, прыжки на батуте, отчасти прыжки на лыжах с трамплина и легкоатлетические прыжки в высоту и длину. Несколько обособленное место занимают в гимнастике маховые и круговые движения, выполняемые на коне с ручками. Это объясняется тем, что в упражнениях на коне оси, вокруг которых вращается тело гимнаста, чаще всего являются промежуточными, т. е. не главными центральными осями инерции. Кроме того, эти оси подвижны и в пространстве и в самом теле спортсмена. Все это сильно осложняет проведение строгого анализа движений, но не делает его невозможным. Упражнения на бревне сочетают в себе элементы вольных и акробатических упражнений, а также опорных прыжков (различные «вскоки»). С точки зрения удержания равновесия все они являются упорами, хотя терминологическое название «упор» имеют лишь немногие из них, в основном простейшие, типа упор на одном колене, упор присев, упор лежа. Все упражнения на бревне являются неустойчивыми равновесиями. Оси, вокруг которых происходят вращения (типа поворотов, кувырков, сальто и переворотов), могут быть подвижными и неподвижными. Перечисленные факты усложняют анализ, но также не вносят ничего нового, не свойственного другим упражнениям. В перечисленных выше видах спорта и гимнастического многоборья многие движения спортсменов протекают в соответствии с законом сохранения момента импульса. При безопорных положениях этот закон проявляется в «чистом» виде, но он действует и в опорных положениях, только в этих слу- чаях его проявления не столь очевидны, они вуалируются внешними силами, такими, как сила земного тяготения, сила трения, сила сопротивления внешней среды (например, воздуха). Закон этот формулируется таким образом: в замкнутой (изолированной) системе момент количества движения есть величина постоянная.
где М — момент количества движения (момент импульса); J —■ момент инерции (величина, равная тг2); о) — угловая скорость. Из механики известно, что линейная скорость пропорциональна радиусу, т. е. v = cor. Отсюда получается, что to = vlr. Подставив это в формулу для момента количества движения и помня, чему равна величина момента инерции, получим:
В этом выражении М — момент количества движения, т — масса, v — линейная скорость точки вращающегося тела, /- — радиус вращающейся точки, т. е. расстояние от оси вращения. Произведение то носит в механике название «количества движения» (или «импульса») и является мерой механического движения. Поскольку масса постоянна, то алгебраически ясно, что для сохранения постоянства величины М скорость и радиус должны изменяться строго обратно пропорционально. Произвольно спортсмен может изменить только радиус (например, группируясь или разгруппировываясь). Из формулы ясно, что если радиус укоротился на величину Аг, то линейная скорость должна увеличиться на ту же величину, чтобы произведение (в соответствии с законом) осталось неизменным. Таким образом, формула показывает, как связаны между собою величины г и v, но она ничего не говорит о том, почему эта связь имеет место. А вопрос этот важный. Действительно, если в процессе группировки увеличиваются скорости всех точек вращающегося тела, то, значит, происходит
изменение скорости, изменение скорости означает, что появилось ускорение. Ускорение, как известно, является следствием действия силы. Откуда же появилась эта сила, если мы рассматриваем систему изолированную, т. е. как раз такую, на которую внешние силы по условию не действуют? На этот вопрос можно ответить, если разобраться в эффектах, впервые объясненных французским физиком Кориолйсом. На рис. 75 изображен диск, вращающийся
вокруг оеи, перпендикулярной чертежу. В точках А и Б этого диска расположены грузики, имеющие одинаковые массы и способные во время вращения перемещаться вдоль радиуса. Пока грузики находятся на периферии, их линейные скорости, обозначенные стрелками, будут максимальными. Скорости остальных точек, расположенных на радиусе, будут уменьшаться по мере приближения к оси вращения пропорционально уменьшению радиуса, т. е. так, как это показано на рисунке. Теперь представим себе, что грузики при неостанавливающемся вращении диска переместились из точек А и Б соответственно в точки At и Б4, линейные скорости которых первоначально были меньше, чем скорости точек А и Б. Грузики в силу инерции сохраняют свою первоначальную скорость и как бы подталкивают лежащие под ними точки А4 и Б4, увеличивая таким образом их скорость. Силы, изменяющие скорости А4 и Bt, носят название сил инерции Кориолиса. Понимание этого факта дает возможность ответить на вопрос, почему имеют место те соотношения, которые описываются формулой сохранения момента количества движения. Если знать, как взаимодействуют между собой величины скорости и радиуса, а также иметь в своем распоряжении данные обо всех силах, действующих одновременно на вращающееся тело (об изменяющемся моменте силы тяжести, о силе реакции опоры, силе трения и сопротивления воздуха), то в этом случае закон сохранения момента импульса может быть применен и к изучению вращение тел несвободных, неизолированных. Во вращательных движениях роль массы заменяется так называемым моментом инерции. Момент инерции — это мера сопротивления тела вращательному движению, так же как масса — мера сопротивления прямолинейному движению. В применении к гимнастическим упражнениям сказанное выше нужно понимать таким образом: если гимнаст во время исполнения любых вращательных движений сгибается (а по предварительному условию любое маховое упражнение является вращательным движением), то он неизбежно изменяет момент инерции своего тела относительно оси вращения. Изменение момента инерции столь же неизбежно приводит к изменению угловой скорости. Эта скорость, если она повышается, дает спортсмену возможность выполнить вращение таким образом, чтобы приземлиться на ноги при исполнении соскока (или завершить необходимое вращение при исполнении оборота). Наоборот, если гимнаст чувствует, что вращение избыточно («перекрут»), тогда при хорошей подготовке (практически — интуитивно) спортсмен разгруппировывается, выпрямляется и таким образом уменьшает угловую скорость своего вращения. Второй закон, который должен учитываться при анализе техники гимнастических упражнений, — это закон сохранения количества движения (закон сохранения импульса). Закон сохранения количества движения так же важен при изучении прямолинейных движений, как закон сохранения момента количества движения для вращательных. Но поскольку прямоли-
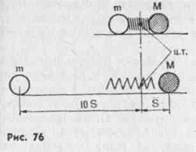
нейных движений в спортивной гимнастике значительно меньше, чем вращательных, то и необходимость приложения этого закона значительно меньше. Он в основном применяется при изучении толчков руками и ногами. Уяснить сущность этого закона проще всего на механической модели. Представим себе совершенно гладкую горизонтальную поверхность, на которой лежат два шара одинаковых размеров, но различных масс (рис. 76). Допустим, что масса М правого шара больше массы т левого шара в 10 раз, т. е. что имеет место равенство \0т = М. Между шарами находится пружина, сжатая внешними силами так, как показано на рисунке. В какой-то момент времени внешняя сила перестает действовать, и шары предоставляются сами себе. Они, очевидно, раскатятся в разные стороны и пройдут пути, обратно пропорциональные их массам. Условно назовем путь, пройденный левым шаром, отрицательным путем, а путь правого шара — положительным*. Если путь, пройденный левым (более легким) шаром, обозначить S, а путь правого (более тяжелого) шара s, то после измерения путей обнаружится, что mS = Ms. Но путь есть произведение скорости на время, т. е. s = vt. Подставив это значение пути в предыдущее равенство, а также учтя, что скорость — вектор, получим новое равенство:
После сокращения на время будем иметь: mV = — Ma. В последнем равенстве произведение массы на скорость уже знакомая нам величина, называемая количеством движения или импульсом. Мы видим, что правая и левая части равенства равны между собой по абсолютной величине, но противоположны по знаку. Это значит, что их сумма равна нулю. Закон сохранения количества движения утверждает, что в изолированной системе количество движения остается постоянным и никакими внутренними * Упрощая рассуждения, мы сознательно игнорируем тот факт, что рассмотренная система не является изолированной, поскольку на нее действует внешняя сила тяжести. Но эта сила уравновешена реакцией опоры, и поэтому ее присутствие не рассматривается.
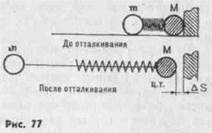
Если же система не изолирована, то эффект будет иным. Рассмотрим это на аналогичной модели. На рис. 77 показаны те же два шара, но теперь правый шар (более тяжелый) упирается в вертикальную стенку. Кроме того, шары связаны между собою нитью, более длинной, чем несжатая пружина. Опыт проводится так же, как в первый раз: пружина вначале сжимается, а затем резко освобождается. Поскольку правому шару откатываться некуда, то, естественно, двигаться будет только левый шар. По инерции он будет катиться и после того, как пружина уже перестанет его толкать. Это будет продолжаться до тех пор, пока не натянется нить, связывающая шары. Как только это случится, левый шар (хотя и более легкий) увлечет за собой правый и оттянет его на какое-то расстояние от вертикальной стенки. Иными словами, энергия движения левого шара в какой-то мере перераспределится и на правый, более тяжелый шар, заставив его двигаться. Подобное явление перераспределения энергии очень часто используется в спортивных движениях вообще и в гимнастике в частности. Так, например, заканчивая толчок о мостик при выполнении опорного прыжка (и вообще всякого прыжка вверх), гимнаст резко поднимает руки вверх. Этим он добивается того, что часть энергии, приобре» тенной руками еще в опоре, передается всему телу, способствуя более высокому взлету. Важно понять, что такое движение рук приводит к желаемому результату только в том случае, когда оно заканчивается еще в опорном положении: бросок руками вверх в полете приведет к тому, что в^е остальные части тела, кроме рук, опустятся вниз относительно о.ц.т. При этом, конечно, все части тела пройдут вниз путь настолько меньший, чем руки вверх, насколько масса всего тела больше массы рук. Мы привели в качестве иримера только одно движение — бросок руками. Но те же рассуждения останутся справедливыми при анализе необходимости резкого разгибания в коленных суставах при выполнении курбета, броска ногами вперед-вверх с последующим торможением при выполнении подъема разгибом на брусьях из упора на руках согнувшись, кувырка назад в стойку на руках в вольных упражнениях и многих других гимнастических упражнений. 8.1.2.1. Структура маховых упражнений В любом маховом упражнении можно выделить 3 фазы действий: а) фазу подготовительных действий — принятие наиболее ра б) фазу основных действий — момент приложения максималь
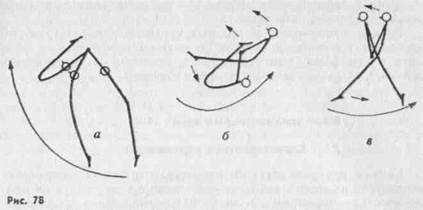
в) фазу завершающих действий (придание движению окончательной формы). Рассмотрим эти фазы на примере двух наиболее известных упражнений — подъема разгибом на перекладине и подъема махом вперед на брусьях. Подъем разгибом на высокой перекладине (рис 78, а, б, в). На рисунках стрелками обозначены: а) фаза подготовительных действий, состоящая из небольшого б) фаза основных действий, которая включает в себя разгиба в) фаза. завершающих действий — выход в упор и его удержа Подъем махом вперед из упора на руках на брусьях (рис. 79):
а) фаза подготовительных б) фаза основных действий —
в) фаза завершающих действий — принятие конечного положения (например, разведение ног для седа ноги врозь). Знание закономерностей маховых упражнений и их структуры позволяет проанализировать любое маховое упражнение и выделить в нем фазы подготовительных, основных и завершающих действий, что очень важно в процессе обучения.
|