Прямоугольная изометрическая проекция
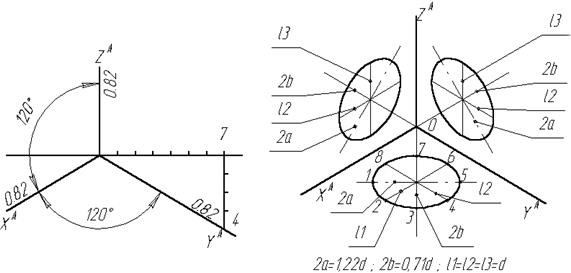
Положение аксонометрических осей изометрической проекции приведено на рис.3.
Рис. 3 Рис. 4
Коэффициенты искажения по осям X, Y, Z равны между собой и численно равны величине аксонометрической единицы. В данном случае u=v=w= 0,82 Как правило, изометрическую проекцию выполняют без искажения, т.е. u=v=w= 1 В этом случае изображение предмета получается увеличенным в 1/0,82 Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.4). При выполнении изометрической проекции без искажения по осям, большая ось эллипсов (БОЭ) равна 1,22, а малая ось (МОЭ) – 0,71 диаметра(d) заданной окружности: БОЭ=2 a =1,22 d; МОЭ=2 b =0,71 d. При этом БОЭ перпендикулярна той координатной оси, которая отсутствует в плоскости окружности. МОЭ перпендикулярна БОЭ, т.е. направлена по координатной оси.
Изометрической проекцией сферы будет окружность с диаметром равным 1,22 диаметра проецируемой сферы (рис.5). Изометрическая проекция наиболее удобна для деталей криволинейной формы, так как обеспечивает достаточную наглядность в сочетании с простотой построения. Эту проекцию целесообразно применять в тех случаях, когда присущий ей большой наклон может выявить скрытые особенности предмета и если при изображении предмета необходимо построить окружности в двух или трех плоскостях, параллельных координатным осям.
|

 1,22 раза. Таким образом, аксонометрический масштаб такого изображения МА1,22:1.
1,22 раза. Таким образом, аксонометрический масштаб такого изображения МА1,22:1.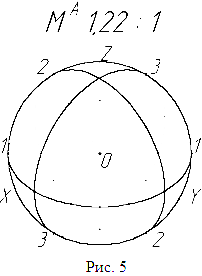 Таким образом, эллипс как аксонометрию окружности в самом простом варианте можно построить по восьми точкам, ограничивающим его большую, малую оси и проекции диаметров, параллельных координатным осям.
Таким образом, эллипс как аксонометрию окружности в самом простом варианте можно построить по восьми точкам, ограничивающим его большую, малую оси и проекции диаметров, параллельных координатным осям.


