Аксонометрические проекции. Рассмотренные нами ортог

Аксонометрические проекции.

 

 

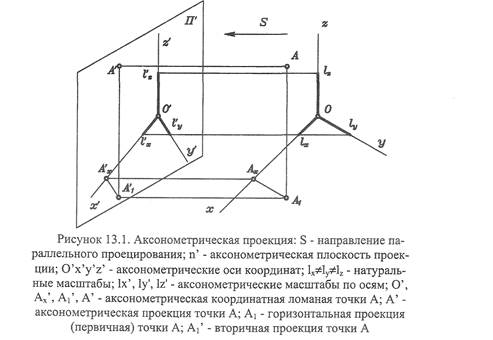
Рассмотренные нами ортог. проекции находят широкое применение при составлении чертежей. С помощью чертежей, построенных в ортог.проекци­ях, если их дополнить вспомогательными изображениями (видами, разрезами и сече­ниями), можно получить представление о форме изображаемого предмета, его конст­рукции, размерах. Наряду с отмеченными достоинствами такой чертеж имеет сущест­венный недостаток - он мало нагляден.

В ряде случаев бывает необходимо наряду с чертежом в ортог. проекци­ях иметь наглядное изображение детали или машины. Такое изображение можно полу­чить с помощью акс. проекции.

Аксонометрия - это чертеж, состоящий из одной // проекции оригинала с изображением осей натуральной системы координат, к которой отнесен это оригинал.

Отнесем точку А к натуральной системе координат. Положение точки А относи­тельно системы координат O_xyz определяется пространственной координатной ломан­ной OA_xA₁ A (рис. 13.1). Координата есть отношение отрезка к масштабу.

 

Натуральные координаты точки А:

Аксонометрические координаты есть отношение акс. отрезка к натуральному масштабу. Акс. координаты точки А:

Показатель искажения - это отношение акс. координаты к нату­ральной или отношение акс. отрезков по акс. осям к на­туральным отрезкам по координатным осям. Показатель искажения изображения по акс. осям:

Из формулы (13.1) находят акс координаты, зная показатели ис­каженна по осям:

х' =U-x; y'=V-y; z'=W-z (13.2)

Формулами (13.2) пользуются для построения акс..

Итак, акс. чертеж строится по координатам, т.е. он осеизмеримый. Очевидно, принимая различное взаимное расположение натуральной системы коорди­нат и акс. Пл. проекции π’ и задавая разные направления про­ецирования, можно получить множество акс. проекций.