Оценка параметра называется несмещённой, если её математическое ожидание М( *) равно неизвестному оцениваемому параметру .2. Оценка 3. Статистическая оценка называется эффективной, если при заданном “n” она имеет наименьшую дисперсию. Выборочная средняя - Несмещённая оценка дисперсии – исправленная выборочная дисперсия - Метод моментов для точечной оценки параметров распределения. Предполагаем, что известен вид функции распределения исследуемой случайной величины (например, равномерное дискретное, или непрерывное экспоненциальное или нормальное и т.д.). Для определения неизвестных параметров этого известного распределения составляем уравнения, в левой части которых – теоретические, а в правых – эмпирические моменты одинаковых порядков. Число таких уравнений равно числу неизвестных параметров распределения (для равномерного -2, для показательного – 1, для нормального – 2 и т. д.)
Метод наибольшего правдоподобия для точечной оценки параметров распределения. Составляем функцию правдоподобия дискретной случайной величины, аргументы которой – полученные выборочным методом значения случайной величины и оцениваемый параметр распределения. Исследуем эту функцию, или, если это удобнее, логарифм функции правдоподобия на экстремум и находим значение оценки, при которой функция достигает максимума. Эта оценка – оценка наибольшего правдоподобия. Доверительный интервал – случайный интервал, в пределах которого с вероятностью 1.Доверительный интервал для оценки мат ожидания СВ
2.Доверительный интервал для оценки среднеквадратического отклонения СВ
|
* называется состоятельный, если она сходится по вероятности к оцениваемому параметру 
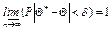
- является несмещённой и состоятельной оценкой математического ожидания.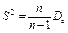
.
; DB 
для равномерного;
для нормального; 
для экспоненциалього.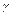
находится неизвестный оцениваемый параметр. 
.
< 
< 
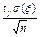, где 
, где s –несмещённое выборочное среднеквадратичное отклонение, q – табличная функция, зависящая от объёма выборки n и надёжности оценки 
