Пространственная и временная дисперсия.

/ОЭП-17/

1) не задаваясь конкретной моделью среды, из общих соображений:

можно утверждать, что в линейной электродинамике эта связь должна иметь вид

 

Аналогично для величин D и Е

 

В этих соотношениях, называемых материальными уравнениями линейной электродинамики, учтено, что состояние среды (индуцированные в ней заряды и токи) в заданный момент времени t в точке пространства г может зависеть от значения поля во все предшествующие моменты времени (в соответствии с принципом причинности) и от значения поля в любой точке среды.

Именно в этом проявляется частотная (временная) и пространственная дисперсия среды. Физически частотная дисперсия связана с инерцией зарядов и процессами релаксации поля в среде, а пространственная дисперсия — с передачей действия поля из одной точки среды в другую из-за наличия в плазме процессов переноса и теплового движения частиц.

Функции называемые часто функциями влияния и представляющие собой ядра интегральных со- соотношений 5.6) и 5.7), характеризуют эффективность передачи действия поля из одной точки пространства — времени в другую. Задачей конкретной модели среды как раз и является нахождение явного выражения этих функций.

/ОЭП-20/

2) Обратимся теперь к анализу материальных уравнений для плазмы, т. е. изучим общий вид и общие свойства функциональных связей 5.6) и 5.7) без получения явного вида этих связей для какой-либо конкретной модели плазмы.

Рассмотрим соотношение 5.6) и 5.7) для случая однородной в пространстве и во времени среды. Однородность во времени означает, что среда не меняет своих свойств во времени под действием внешних причин, не связанных с действием электромагнитного поля. Очевидно, в этом случае ядра интегральных соотношений 5.6) и 5.7) являются разностными функциями времени и координат, т. е. зависят от и

Зависимость этих тензоров от и определяет частотную (временную)

дисперсию, а зависимость их от волнового вектора к — пространст-

пространственную дисперсию электромагнитного поля в среде.

 

 

И стр 27-29

Отсутствие дисперсии

Электрон колеблется в определенной точке пространства с определенной частотой. Поэтому частота электрона в некотором смысле несет информацию о данной точке в данный момент времени. Если электрон движется в такой области, что при этом взаимодействует с другими электронами, и соответственно, передает им и принимает от них информацию об окружающих точках в фиксированные моменты времени, то в этом случае есть дисперсия. Если же такого взаимодействия нет, то нет дисперсии.

Математически отсутствие дисперсии можно записать, домножив подинтегральное выражение

на дельта-функцию (обрежутся все шрихованные зависимост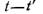и)