Пусть неизвестный параметр распределения наблюдаемой случайной величины  векторный:
векторный:  и у случайной величины
и у случайной величины  существует конечный r-ый момент:
существует конечный r-ый момент: 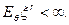
Оценкой неизвестного параметра  , полученной методом моментов (ОММ), называется вектор
, полученной методом моментов (ОММ), называется вектор 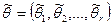 , где
, где 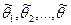 есть решение системы уравнений:
есть решение системы уравнений:

Теоретические моменты, являющиеся функциями от неизвестных параметров  , приравниваются к их статистическим аналогам – выборочным моментам. Полученная система – это система r уравнений с r переменными. Если решения системы уравнений нет, оценки по методу моментов не существует. Если имеется несколько решений, то существует несколько таких оценок. Если система уравнений имеет единственное решение, то оценка по методу моментов является состоятельной оценкой параметра
, приравниваются к их статистическим аналогам – выборочным моментам. Полученная система – это система r уравнений с r переменными. Если решения системы уравнений нет, оценки по методу моментов не существует. Если имеется несколько решений, то существует несколько таких оценок. Если система уравнений имеет единственное решение, то оценка по методу моментов является состоятельной оценкой параметра  .
.
-

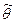 находят из условия:
находят из условия: 
-

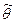 находят из условия:
находят из условия: 
-

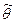 находят из условий:
находят из условий: 
Оценка максимального правдоподобия 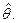
Оценкой максимального правдоподобия неизвестного параметра  (в общем случае это векторный параметр) называется такая точка параметрического пространства, на которой функция правдоподобия на полученной реализации выборки достигает своего максимума:
(в общем случае это векторный параметр) называется такая точка параметрического пространства, на которой функция правдоподобия на полученной реализации выборки достигает своего максимума:
 ,
, 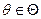
Если  -векторный параметр, максимум функции правдоподобия
-векторный параметр, максимум функции правдоподобия  для любой реализации выборки достигается во внутренней точке параметрического множества, и функция правдоподобия дифференцируема по каждой переменной
для любой реализации выборки достигается во внутренней точке параметрического множества, и функция правдоподобия дифференцируема по каждой переменной 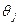 , тогда:
, тогда:
Оценкой максимального правдоподобия неизвестного векторного параметра  называется вектор
называется вектор  , где
, где  есть решение системы уравнений правдоподобия
есть решение системы уравнений правдоподобия
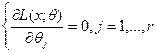
или системы уравнений правдоподобия
 .
.
ü Пусть  - выборка из равномерного распределения
- выборка из равномерного распределения  . В данном случае оценка максимального правдоподобия
. В данном случае оценка максимального правдоподобия  , состоятельная, и её закон распределения
, состоятельная, и её закон распределения  , то есть в данном случае распределение
, то есть в данном случае распределение  не является асимптотически нормальным (модель не регулярная).
не является асимптотически нормальным (модель не регулярная).
ü В случае модели  любое значение
любое значение  является оценкой максимального правдоподобия
является оценкой максимального правдоподобия 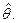 Средняя точка интервала, то есть
Средняя точка интервала, то есть  , является несмещенной оценкой θ.
, является несмещенной оценкой θ.
Доверительный интервал для параметра.
СВ  U
U 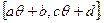
Построим доверительный интервал для параметра  с заданной доверительной вероятностью γ.
с заданной доверительной вероятностью γ.
Для этого введём новую СВ  Тогда
Тогда 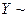 U
U  U
U 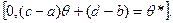 Сначала построим такой доверительный интервал для параметра θ*.
Сначала построим такой доверительный интервал для параметра θ*.
Рассмотрим СВ 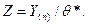
 - это для
- это для  функция распределения максимума выборки n равномерно распределенных случайных величин на [0,1]
функция распределения максимума выборки n равномерно распределенных случайных величин на [0,1]  . Распределение СВ Z не зависит от θ*, значит, и от θ, поэтому СВ Z – центральная статистика. Наивероятнейшие значения Z в окрестности 1. Тогда доверительный интервал для Z будет иметь вид
. Распределение СВ Z не зависит от θ*, значит, и от θ, поэтому СВ Z – центральная статистика. Наивероятнейшие значения Z в окрестности 1. Тогда доверительный интервал для Z будет иметь вид  то есть
то есть
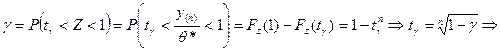
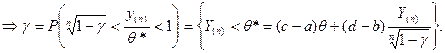
Или с вероятностью γ выполняются неравенства:
 или
или

 или
или
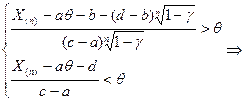
 - искомый доверительный интервал для параметра θ с доверительной вероятностью γ.
- искомый доверительный интервал для параметра θ с доверительной вероятностью γ.
ü В модели  по выборке объёма n γ-доверительный интервал для параметра θ будет таким:
по выборке объёма n γ-доверительный интервал для параметра θ будет таким:  .
.
ü В модели  γ-доверительный интервал будет таким:
γ-доверительный интервал будет таким:  .
.
Асимптотические свойства о.м.п.
Пусть Х=( - выборка из распределения U(0,θ). Тогда о.м.п.
- выборка из распределения U(0,θ). Тогда о.м.п.  =
=  .
.
Рассмотрим вспомогательный пример.
Пусть F(x) = x, 0 ≤ x ≤ 1. Здесь 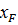 =1 и применим критерий
=1 и применим критерий  с α=1; при этом
с α=1; при этом  =
=  ,
,  =1. Таким образом, в данном случае имеем предел:
=1. Таким образом, в данном случае имеем предел:
P{ n ( ─ 1) ≤ x } →
─ 1) ≤ x } →  , x<0.
, x<0.
Возвращаясь к исходной задаче видим, что экстремальные значения выборки не являются асимптотически нормальными. В частности, в рассматриваемом примере имеем (т.к.  (ξ/θ)=U(0,1)):
(ξ/θ)=U(0,1)):
 ={ n (
={ n ( ─ 1)≤ x } →
─ 1)≤ x } →  , x<0.
, x<0.

 векторный:
векторный:  и у случайной величины
и у случайной величины 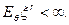
 , полученной методом моментов (ОММ), называется вектор
, полученной методом моментов (ОММ), называется вектор 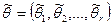 , где
, где 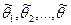 есть решение системы уравнений:
есть решение системы уравнений:
 , приравниваются к их статистическим аналогам – выборочным моментам. Полученная система – это система r уравнений с r переменными. Если решения системы уравнений нет, оценки по методу моментов не существует. Если имеется несколько решений, то существует несколько таких оценок. Если система уравнений имеет единственное решение, то оценка по методу моментов является состоятельной оценкой параметра
, приравниваются к их статистическим аналогам – выборочным моментам. Полученная система – это система r уравнений с r переменными. Если решения системы уравнений нет, оценки по методу моментов не существует. Если имеется несколько решений, то существует несколько таких оценок. Если система уравнений имеет единственное решение, то оценка по методу моментов является состоятельной оценкой параметра  .
.
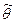 находят из условия:
находят из условия: 




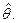
 ,
, 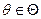
 для любой реализации выборки достигается во внутренней точке параметрического множества, и функция правдоподобия дифференцируема по каждой переменной
для любой реализации выборки достигается во внутренней точке параметрического множества, и функция правдоподобия дифференцируема по каждой переменной 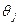 , тогда:
, тогда: , где
, где  есть решение системы уравнений правдоподобия
есть решение системы уравнений правдоподобия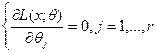
 .
. - выборка из равномерного распределения
- выборка из равномерного распределения  . В данном случае оценка максимального правдоподобия
. В данном случае оценка максимального правдоподобия  , состоятельная, и её закон распределения
, состоятельная, и её закон распределения  , то есть в данном случае распределение
, то есть в данном случае распределение  не является асимптотически нормальным (модель не регулярная).
не является асимптотически нормальным (модель не регулярная). любое значение
любое значение  является оценкой максимального правдоподобия
является оценкой максимального правдоподобия  , является несмещенной оценкой θ.
, является несмещенной оценкой θ. U
U 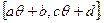
 с заданной доверительной вероятностью γ.
с заданной доверительной вероятностью γ. Тогда
Тогда 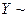 U
U  U
U 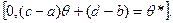 Сначала построим такой доверительный интервал для параметра θ*.
Сначала построим такой доверительный интервал для параметра θ*.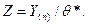
 - это для
- это для  функция распределения максимума выборки n равномерно распределенных случайных величин на [0,1]
функция распределения максимума выборки n равномерно распределенных случайных величин на [0,1]  . Распределение СВ Z не зависит от θ*, значит, и от θ, поэтому СВ Z – центральная статистика. Наивероятнейшие значения Z в окрестности 1. Тогда доверительный интервал для Z будет иметь вид
. Распределение СВ Z не зависит от θ*, значит, и от θ, поэтому СВ Z – центральная статистика. Наивероятнейшие значения Z в окрестности 1. Тогда доверительный интервал для Z будет иметь вид  то есть
то есть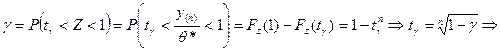
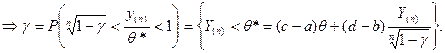
 или
или
 или
или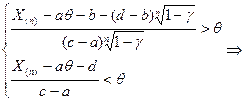
 - искомый доверительный интервал для параметра θ с доверительной вероятностью γ.
- искомый доверительный интервал для параметра θ с доверительной вероятностью γ. .
. γ-доверительный интервал будет таким:
γ-доверительный интервал будет таким:  .
. - выборка из распределения U(0,θ). Тогда о.м.п.
- выборка из распределения U(0,θ). Тогда о.м.п.  =
=  .
.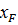 =1 и применим критерий
=1 и применим критерий  с α=1; при этом
с α=1; при этом  =
=  ,
,  =1. Таким образом, в данном случае имеем предел:
=1. Таким образом, в данном случае имеем предел: ─ 1) ≤ x } →
─ 1) ≤ x } →  , x<0.
, x<0. (ξ/θ)=U(0,1)):
(ξ/θ)=U(0,1)): ={ n (
={ n ( ─ 1)≤ x } →
─ 1)≤ x } → 


