Векторное управление асинхронным приводом

Как и во всяком электромеханическом преобразователе, момент асинхронного двигателя является функцией произведения векторов потока ротора и статора, приведенных в одну систему координат. Следовательно, если мы сформируем эти векторы и будем регулировать их модуль или угол между ними, то мы можем изменять момент и скорость двигателя. Такое управление называют векторным управлением асинхронным приводом. В нем аналогично с приводом постоянного тока возможно раздельное регулирование потока и тока двигателя, что обеспечивает как предельное быстродействие, так и высокую экономичность регулирования. В двигателях постоянного тока момент является векторным произведением тока якоря на потокосцепление обмотки якоря с обмоткой возбуждения. Но, так как здесь угол между векторами тока и потокосцепления путем настройки коммутации поддерживается постоянным и равным π/2, при котором обеспечивается максимум момента при минимуме потребляемой мощности, момент определяется скалярным произведением тока якоря на поток возбуждения (2.5).

В асинхронном двигателе ток ротора создается путем передачи энергии индукционным методом со стороны статора. Поэтому для того чтобы осуществить независимое регулирование потока Φ=f(ix) и момента M=F(iy), где ix и iy независимые переменные, необходимо соответствующим образом регулировать токи фаз статора. Однако при этом возникает задача определения основных координат привода: фазных токов и напряжений; скорости вращения ротора; положения вектора н.с. ротора и статора и т.д., некоторые из которых не доступны для прямого измерения. Появление микропроцессорных средств позволило вычислять координаты привода, недоступные для измерения, и реализовать законы управления, более сложные, но более эффективные.

Для упрощения понимания принципа векторного управления обратимся к упрошенной модели асинхронного двигателя, для чего примем ряд допущений. Прежде всего, будем считать, что асинхронный двигатель работает при малых скольжениях, поэтому цепь ротора можно считать чисто активной. В результате на векторной диаграмме рис. 3.2, вектор тока I2', будет совпадать с вектором E2', следовательно, и с вектором E1. Такое допущение справедливо, так как в номинальном режиме отклонение вектора тока ротора от вектора его ЭДС не превышает 10÷15 градусов. Кроме того, пренебрежем падением напряжения в обмотке статора, т.е. примем U1≈E1. С учетом принятых допущений векторная диаграмма асинхронного двигателя получит вид рис. 5.4.

Электромагнитный момент в асинхронном двигателе возникает в результате взаимодействия вектора поля статора, который совпадает с вектором тока намагничивания Iμ и вектором поля ротора, который совпадает с вектором тока ротора I2'. При этом регулирование тока намагничивания эквивалентно регулированию тока возбуждения, а регулирование тока ротора эквивалентно регулированию тока якоря в двигателе постоянного тока независимого возбуждения.

Для того чтобы сформировать независимые векторы потоков ротора и статора, рассмотрим приближенные соотношения связи токов, напряжений и ЭДС двигателя. В частности, в п. 3.1.5. мы показали, что напряжение и ЭДС статора связаны с током намагничивания соотношением

(5.1)

U1≈E1=k1f1Iμ,

где k1 – коэффициент связи между ЭДС статора и током намагничивания, f1 – частота напряжения питания статорной цепи, Iμ – ток намагничивания.

Рис. 5.4. Упрощенная векторная диаграмма асинхронного двигателя

Согласно рис.5.4. имеем

(5.2)

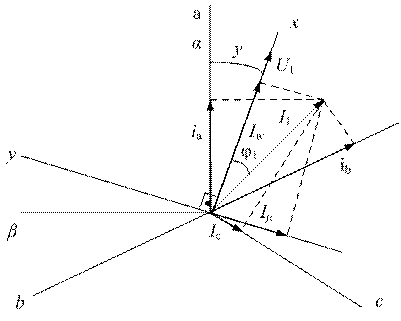
где I1а – активная составляющая тока статора, I2' – приведенный ток ротора, I1 – ток статора.

Кроме того, ток ротора можно определить по соотношению

(5.3)

I2'=E2'/r2=k1f1sIμ,

где E2' – приведенная ЭДС ротора, s – скольжение.

Связь между частотой вращения ротора и частотой сети записывается выражением

ω=2πf1s.

Нам необходимо определить текущие значения s, I1а и Iμ. Для этого воспользуемся приведенными уравнениями. По измеренному значению f1 и U1 из (5.1) определим Iμ. По рассчитанному значению Iμ и измеренному значению I1 из уравнения (5.2) найдем I1а. Напомним, что нашей задачей является независимое регулирование тока намагничивания и тока ротора. Обе этих координаты являются функцией двух независимых переменных: напряжения статора – U1 и частоты f1. Очевидно, что можно найти такой закон изменения каждой из независимых переменных, который позволит регулировать лишь одну из указанных координат при постоянном значении другой.

В выражениях (5.1 – 5.3) используются амплитудные или действующие значения результирующих векторов напряжений и токов. В реальной схеме с помощью датчиков мы можем зафиксировать только фазные действующие напряжения питания двигателя. Поэтому появляется необходимость восстановления результирующих векторов по фазовым значениям координат. На рис. 5.5 представлены неподвижные системы координат: трехфазная – с осями a, b и c и двухфазная – с осями α и β, причем ось α направлена по оси a. Там же изображена подвижная, вращающаяся с частотой поля статора система координат с осями x и y. Причем ось x направлена по оси изображающего вектора U1. Чтобы не загромождать рисунок покажем процедуру вычислений только вектора U1. По измеренным мгновенным значениям фазных напряжений определяются проекции вектора U1 на оси α и β и по ним определяется модуль этого вектора и его угол поворота γ относительно оси α. Точно также определяется вектор тока I1. Причем его составляющие I1а и Iμ определяются как проекции на ось x и y соответственно.

Рис. 5.5. Векторная диаграмма асинхронного двигателя в различных системах координат

Векторное управление асинхронным двигателем обеспечивает точное поддержание электромагнитного момента и устойчивую работу во всем диапазоне скоростей, включая работу на упор. В настоящее время серийно выпускаются частотные преобразователи, реализующие векторное управление, реализующие изложенные выше принципы проектирования, – достаточно выбрать удовлетворяющий, предъявляемым к приводу требованиям.

5.2. Система управляемый преобразователь – синхронный двигатель

В предыдущем параграфе мы показали – для того, чтобы приблизить по свойствам электропривод с асинхронным двигателем к приводу на основе двигателя постоянного тока, необходимо обеспечить ортогональность и независимость регулирования векторов поля ротора и статора, как это имеет место в двигателе постоянного тока. При этом в связи с тем, что в асинхронном двигателе магнитное поле ротора создается за счет энергии, поступающей со статора, и может быть как угодно ориентировано относительно осей ротора, для обеспечения ортогональности и независимости регулирования полей требуются достаточно сложные и дорогостоящие схемные решения, которые могут быть оправданы только в приводах большой мощности (десятки и сотни киловатт).

В синхронном двигателе магнитное поле ротора создается либо обмоткой возбуждения, либо постоянными магнитами. Отсюда естественно появляется возможность их независимого регулирования. Следовательно, система частотного управления здесь может быть реализована просто – достаточно включить двигатель на управляемый преобразователь частоты. Однако в таком виде системы частотного управления синхронными двигателями используются относительно редко. Это связано с тем, что при выходе двигателя из синхронизма, например, в результате вешнего воздействия со стороны нагрузки, не всегда возможно или достаточно сложно восстановить синхронный режим. Выход из синхронизма приводит к тому, что вектор поля ротора начинает вращаться относительно вектора поля статора. Следовательно, для того, чтобы исключить такое явление, переключение ключей преобразователя частоты необходимо связать с положением ротора двигателя относительно статора так, чтобы угловое рассогласование векторов оставалось неизменным, и, как у коллекторного двигателя постоянного тока, его можно установить равным π/2. В связи с этим синхронный двигатель, работающий от преобразователя частоты, подключенного к источнику постоянного тока, и имеющий обратную связь по положению ротора, называют вентильным двигателем постоянного тока (ВД). Наиболее просто такие двигатели реализуются при возбуждении ротора от постоянного магнита. В этом случае ВД может быть выполнен бесконтактным и сочетает в себе положительные свойства как машин постоянного тока (хорошие регулировочные свойства и отличные энергетические показатели), так и машин переменного тока (большой ресурс, высокую надежность и работоспособность в вакууме, взрывоопасных и ядовитых средах). Вентильные двигатели являются наиболее перспективными в электроприводах летательных аппаратов и систем автоматики, в бытовой и в медицинской технике, т.е. в тех случаях, когда перечисленные положительные свойства являются определяющими.