Уравнения напряжений трансформатора
Основной переменный магнитный поток Ф в магнитопроводе трансформатора, сцепляясь с витками обмоток w1 и w 2 (см. рис. 1.1), наводит в них ЭДС [см. (1.1) и (1.2)]
Предположим, что магнитный поток Ф является синусоидальной функцией времени, т. е.
где Фmax — максимальное значение потока. Тогда, подставив (1.4) в формулу ЭДС е1 и дифференцируя, получим
Но так как
По аналогии,
Из (1.6) и (1.7) следует, что ЭДС е\ и е2 отстают по фазе от потока Ф на угол п/2. Максимальное значение ЭДС
Разделив E1maxна √2 и подставив ω = 2π f, получим действующее значение первичной ЭДС (В):
Аналогично, для вторичной ЭДС
Отношение ЭДС обмотки высшего напряжения к ЭДС обмотки низшего напряжения называют коэффициентом трансформации:
При практических расчетах коэффициент трансформации с некоторым допущением принимают равным отношению номинальных напряжений обмоток ВН и НН:
Рис. 1.14. Магнитные потоки в однофазном трансформаторе
Токи I1 и I2 в обмотках трансформатора помимо основного магнитного потока Ф создают магнитные потоки рассеяния
где Так как магнитные потоки рассеяния замыкаются главным образом в немагнитной среде (воздух, масло, медь), магнитная проницаемость которой постоянна, то и индуктивности Ls1 и Ls2 можно считать постоянными. Действующие значения ЭДС рассеяния пропорциональны токам в соответствующих обмотках:
где x1 и x2 — индуктивные сопротивления рассеяния первичной и вторичной обмоток соответственно, Ом (знак минус в этих выражениях свидетельствует о реактивности ЭДС рассеяния). Таким образом, в каждой из обмоток трансформатора индуцируются по две ЭДС: ЭДС от основного потока Ф и ЭДС от потока рассеяния ( Для первичной цепи трансформатора, включенной в сеть на напряжение
или, перенеся ЭДС
ЭДС первичной обмотки Обычно индуктивное
Для вторичной цепи трансформатора, замкнутой на нагрузку с сопротивлением
т.е. сумма ЭДС, наведенных во вторичной обмотке
Приведем уравнение (1.15) к виду, аналогичному уравнению ЭДС для первичной цепи (1.13). При этом учтем выражения (1.12) и (1.16) и получим уравнение напряжений для вторичной цепи трансформатора:
Из этого уравнения следует, что напряжение на выходе нагруженного трансформатора отличается от ЭДС вторичной обмотки на величину падения напряжений в этой обмотке. Пример 1.2. Имеется однофазный трансформатор (рис. 1.14) номинальной мощностью Определить: числа витков обмоток трансформатора w l и w 2 поперечное сечение обмоточных проводов первичной q 1 и вторичной q 2 обмоток, если плотность тока в этих проводах D =• 4,0 А/мм2; площадь поперечного сечения стержня магнитопровода Qст, если максимальное значение магнитной индукции в стержне Bст, = 1,4Тл. Решение. По номинальным значениям напряжений U1ном, и U2ном определяем числа витков в обмотках: w 1 = U1ном / U2ном = 6000/5 = 1200; w 2 = U2ном jUвит = 400/5 = 80, Номинальные значения токов в обмотках: I 1HOM = Sном /U1 = 100• 103/6000 = 16,7 А; I 2ном = Sном / U 2 = 100• 103/400 = 250 А. Поперечные сечения обмоточных проводов: q1 = I 1HOM /∆ = 16,7/4 = 4,175 мм2; q2 = I 2ном /∆ = 250/4 = 62,5 мм2. Основной магнитный поток в стержне определим, используя выражение (1.10) и учитывая, что номинальное вторичное напряжение U2ном = Е2: Фmax = Е2 /(4,44 fw 2) = 400/(4,44 • 50 • 80) = 0,0225 Вб. Поперечное сечение стержня магнитопровода Qст = Фmax /(kсBст) = 0,0225/(0,93-1,4) = 0,017 м2, где kс = 0,93 — коэффициент заполнения шихтованного стержня сталью, учитывающий увеличение сечения стержня прослойками изоляционного лака между стальными полосами.
|


 , (1.4)
, (1.4) . (1.5)
. (1.5) то
то . (1.6)
. (1.6) , (1.7)
, (1.7)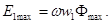 (1.8)
(1.8) (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11)

 и
и 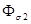 (рис. 1.14), каждый из которых сцеплен с витками лишь собственной обмотки и индуцирует в ней ЭДС рассеяния. Эти ЭДС в первичной и вторичной обмотках таковы:
(рис. 1.14), каждый из которых сцеплен с витками лишь собственной обмотки и индуцирует в ней ЭДС рассеяния. Эти ЭДС в первичной и вторичной обмотках таковы:
 и
и 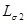 — индуктивности рассеяния.
— индуктивности рассеяния.
 , с учетом падения напряжения в активном сопротивлении первичной обмотки
, с учетом падения напряжения в активном сопротивлении первичной обмотки  можно записать уравнение напряжений по второму закону Кирхгофа:
можно записать уравнение напряжений по второму закону Кирхгофа:
 и
и  в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния
в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния  , получим уравнение напряжений для первичной цепи трансформатора:
, получим уравнение напряжений для первичной цепи трансформатора: (1.13)
(1.13) , наведенная основным магнитным потоком Ф, представляет собой ЭДС самоиндукции, а поэтому находится в противофазе с подведенным к первичной обмотке напряжением
, наведенная основным магнитным потоком Ф, представляет собой ЭДС самоиндукции, а поэтому находится в противофазе с подведенным к первичной обмотке напряжением  и активное
и активное  падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение
падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение  , т. е.
, т. е. (1.14)
(1.14) , уравнение напряжений имеет вид
, уравнение напряжений имеет вид (1.15)
(1.15) , уравновешивается суммой падений напряжений
, уравновешивается суммой падений напряжений  . Здесь
. Здесь  — активное сопротивление вторичной обмотки. Падение напряжения на нагрузке
— активное сопротивление вторичной обмотки. Падение напряжения на нагрузке 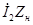 представляет собой напряжение на выводах вторичной обмотки трансформатора:
представляет собой напряжение на выводах вторичной обмотки трансформатора: (1.16)
(1.16) (1.17)
(1.17) и номинальными напряжениями
и номинальными напряжениями  и
и  , при частоте тока f = 50 Гц; действующее значение напряжения, приходящееся на один виток обмоток,
, при частоте тока f = 50 Гц; действующее значение напряжения, приходящееся на один виток обмоток,  .
.


